
【题目】已知Rt△ABC如图(1),∠C=90°,D.E分别是AC,AB的中点,将△ADE沿DE折起到PDE位置(即A点到P点位置)如图(2)使∠PDC=60°.
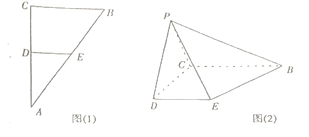
(1)求证:BC⊥PC;
(2)若BC=2CD=4,求点D到平面PBE的距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)证明![]() 垂直平面
垂直平面![]() 中的两条直线
中的两条直线![]() 再证明
再证明![]() 平面
平面![]() 即可.
即可.
(2)取取CD中点![]() 建立空间直角坐标系,再利用空间向量解决点到面的距离问题即可.
建立空间直角坐标系,再利用空间向量解决点到面的距离问题即可.
(1)证明:∵Rt△ABC如图(1),∠C=90°,D.E分别是AC,AB的中点,
将△ADE沿DE折起到PDE位置(即A点到P点位置)如图(2)使∠PDC=60°.
∴DE⊥DC,DE⊥PD,DE∥BC,
∵PD∩DC=D,∴DE⊥平面PCD,∴BC⊥平面PCD,
∵PC平面PCD,∴BC⊥PC.
(2)解:∵D.E分别是AC,AB的中点,∠PDC=60°,BC=2CD=4,
∴CD=PD=PC=2,
取CD中点O,BE中点M,连结PO,MO,则OP,OD,OM两两垂直,
以O为原点,OD为x轴,OM为y轴,OP为z轴,建立空间直角坐标系,
则D(1,0,0),P(0,0,![]() ),B(﹣1,4,0),E(1,2,0),
),B(﹣1,4,0),E(1,2,0),
![]() (1,0,
(1,0,![]() ),
),![]() (﹣1,4,
(﹣1,4,![]() ),
),![]() (1,2,
(1,2,![]() ),
),
设平面PBE的法向量![]() (x,y,z),
(x,y,z),
则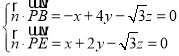 ,取x=1,得
,取x=1,得![]() (1,1,
(1,1,![]() ),
),
∴点D到平面PBE的距离为:
d



科目:高中数学 来源: 题型:
【题目】在如图所示的组合体中,三棱柱![]() 的侧面
的侧面![]() 是圆柱的轴截面,
是圆柱的轴截面,![]() 是圆柱底面圆周上不与
是圆柱底面圆周上不与![]() 重合的一个点.
重合的一个点.
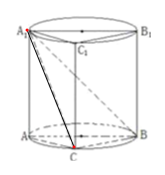
(1)若圆柱的轴截面是正方形,当点![]() 是弧
是弧![]() 的中点时,求异面直线
的中点时,求异面直线![]() 与
与![]() 的所成角的大小;
的所成角的大小;
(2)当点![]() 是弧
是弧![]() 的中点时,求四棱锥
的中点时,求四棱锥![]() 与圆柱的体积比.
与圆柱的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为配合国家“一带一路”战略,发展城市旅游经济,拟在景观河道的两侧,沿河岸直线![]() 与
与![]() 修建景观(桥),如图所示,河道为东西方向,现要在矩形区域
修建景观(桥),如图所示,河道为东西方向,现要在矩形区域![]() 内沿直线将
内沿直线将![]() 与
与![]() 接通.已知
接通.已知![]() ,
,![]() ,河道两侧的景观道路修复费用为每米
,河道两侧的景观道路修复费用为每米![]() 万元,架设在河道上方的景观桥
万元,架设在河道上方的景观桥![]() 部分的修建费用为每米
部分的修建费用为每米![]() 万元.
万元.
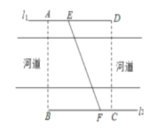
(1)若景观桥长![]() 时,求桥与河道所成角的大小;
时,求桥与河道所成角的大小;
(2)如何景观桥![]() 的位置,使矩形区域
的位置,使矩形区域![]() 内的总修建费用最低?最低总造价是多少?
内的总修建费用最低?最低总造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)令![]() ,已知函数
,已知函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若存在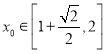 ,使不等式
,使不等式![]() 对任意
对任意![]() (取值范围内的值)恒成立,求实数
(取值范围内的值)恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最,编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”,见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注,还得到了无数外国人的关注.某单位有6位外国人,其中关注此次大阅兵的有5位,若从这6位外国人中任意选取2位做一次采访,则被采访者都关注了此次大阅兵的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是定义在
是定义在![]() 上且满足如下条件的函数
上且满足如下条件的函数![]() 组成的集合:
组成的集合:
①对任意的![]() ,都有
,都有![]() ;
;
②存在常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() .
.
(1)设![]() ,问
,问![]() 是否属于
是否属于![]() ?说明你的判断理由;
?说明你的判断理由;
(2)若![]() ,如果存在
,如果存在![]() ,使得
,使得![]() ,证明这样的
,证明这样的![]() 是唯一的;
是唯一的;
(3)设![]() 为正实数,是否存在函数
为正实数,是否存在函数![]() ,使
,使![]() ?作出你的判断,并说明理由.
?作出你的判断,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com