已知椭圆的长轴是短轴的
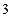
倍,且过点
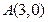
,并且以坐标轴为对称轴,
求椭圆的标准方程。
椭圆的方程为:

或
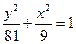
解法一:若椭圆的焦点在

轴上,设方程为

由题意得:

,解得

,∴椭圆方程为

;若焦点在

轴上,设方程为

,由题意得:

,解得

,∴椭圆的方程为
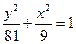
,综上得:椭圆的方程为:

或
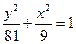
。
解法二:设椭圆的方程为:

,则由题意得:

或
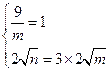
,解得:

或

,所以椭圆的方程为:

或
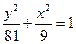
。
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知椭圆

,能否在椭圆上位于

轴左侧的部分找到一点

,使其到左准线

的距离

为点

到两个焦点

的距离的等比中项?说明理由。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
椭圆

上一点

到其左准线的距离为

,那么

点到该椭圆右焦点的距离是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知椭圆
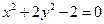
的两焦点为
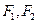
,
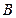
为短轴的一个端点,则
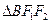
的外接圆的方程是
。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知椭圆
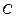
的焦点分别为
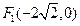
和
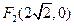
,长轴长为
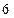
,设直线
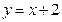
交椭圆
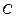
于
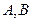
两点,求线段
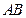
的中点坐标。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分12分)已知椭圆

为常数,且

,过点

且以向量

为方向向量的直线与椭圆交于点

,直线
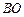
交椭圆于点

(

为坐标原点).(1)

的面积
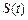
的表达式;(2)若

,求
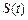
的最大值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
在平面直角坐标系中,椭圆
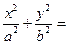
1(
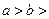
0)的焦距为2,以O为圆心,
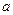
为半径的圆,过点
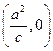
作圆的两切线互相垂直,则离心率
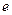
=
.
查看答案和解析>>

 倍,且过点
倍,且过点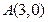 ,并且以坐标轴为对称轴,
,并且以坐标轴为对称轴, 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 为常数,且
为常数,且 ,过点
,过点 且以向量
且以向量 为方向向量的直线与椭圆交于点
为方向向量的直线与椭圆交于点 ,直线
,直线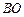 交椭圆于点
交椭圆于点 (
( 为坐标原点).(1)
为坐标原点).(1) 的面积
的面积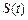 的表达式;(2)若
的表达式;(2)若 ,求
,求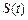 的最大值.
的最大值.