
【题目】已知y=f(x)是定义在(-∞,+∞)上的奇函数,且在[0,+∞)上为增函数,
(1)求证:函数在(-∞,0)上也是增函数;
(2)如果f(![]() )=1,解不等式-1<f(2x+1)≤0.
)=1,解不等式-1<f(2x+1)≤0.
【答案】(1)证明见解析;(2){x|-![]() <x≤-
<x≤-![]() }.
}.
【解析】
(1)设![]() ,且
,且![]() ,根据单调性的定义,结合函数奇偶性,即可得证;
,根据单调性的定义,结合函数奇偶性,即可得证;
(2)根据![]() 是R上的奇函数,把
是R上的奇函数,把![]() ,转化为
,转化为![]() ,再结合函数的单调性,得到
,再结合函数的单调性,得到![]() ,即可求解.
,即可求解.
(1)设x1、x2是(-∞,0]上任意两个不相等的实数,且x1<x2,
则-x1,-x2∈[0,+∞),且-x1>-x2,Δx=x2-x1>0,Δy=f(x2)-f(x1).
因为f(x)是奇函数,且在[0,+∞)上是增函数,-x1>-x2,
所以f(-x1)>f(-x2).
又因为f(x)为奇函数,所以f(-x1)=-f(x1),f(-x2)=-f(x2),
所以-f(x1)>-f(x2),即f(x1)<f(x2),
即Δy=f(x2)-f(x1)>0,
所以函数f(x)在(-∞,0]上也是增函数.
(2)因为f(x)是R上的奇函数,所以f(0)=0,f(-![]() )=-f(
)=-f(![]() )=-1,
)=-1,
由-1<f(2x+1)≤0,得f(-![]() )<f(2x+1)≤f(0).
)<f(2x+1)≤f(0).
又因为f(x)在(-∞,0)上是增函数,所以-![]() <2x+1≤0,解得-
<2x+1≤0,解得-![]() <x≤-
<x≤-![]() ,
,
所以不等式的解集为{x|-![]() <x≤-
<x≤-![]() }.
}.


科目:高中数学 来源: 题型:
【题目】已知曲线C:x2-y2=1及直线l:y=kx-1.
(1)若l与C有两个不同的交点,求实数k的取值范围;
(2)若l与C交于A,B两点,O为坐标原点,且△AOB的面积为![]() ,求实数k的值.
,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() (
(![]() =1,2,…,6),如表所示:
=1,2,…,6),如表所示:
试销单价 | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量 | q | 84 | 83 | 80 | 75 | 68 |
已知![]() .
.
(Ⅰ)求出![]() 的值;
的值;
(Ⅱ)已知变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(参考公式:线性回归方程中![]() ,
,![]() 的最小二乘估计分别为
的最小二乘估计分别为 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的两个焦点分别为F1,F2,离心率为
(a>b>0)的两个焦点分别为F1,F2,离心率为![]() ,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
(1)求椭圆C的方程;
(2)若直线y=kx+b与椭圆C分别交于A,B两点,且OA⊥OB,试问点O到直线AB的距离是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据调查显示,某高校![]() 万男生的身高服从正态分布
万男生的身高服从正态分布![]() ,现从该校男生中随机抽取
,现从该校男生中随机抽取![]() 名进行身高测量,将测量结果分成
名进行身高测量,将测量结果分成![]() 组:
组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并绘制成如图所示的频率分布直方图.
,并绘制成如图所示的频率分布直方图.
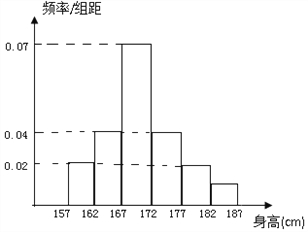
(Ⅰ)求这![]() 名男生中身高在
名男生中身高在![]() (含
(含![]() )以上的人数;
)以上的人数;
(Ⅱ)从这![]() 名男生中身高在
名男生中身高在![]() 以上(含
以上(含![]() )的人中任意抽取
)的人中任意抽取![]() 人,该
人,该![]() 人中身高排名(从高到低)在全校前
人中身高排名(从高到低)在全校前![]() 名的人数记为
名的人数记为![]() ,求
,求![]() 的数学期望.
的数学期望.
(附:参考数据:若![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划销售某种食品,现邀请甲、乙两个商家进场试销10天.两个商家提供的返利方案如下:甲商家每天固定返利60元,且每卖出一件食品商家再返利3元;乙商家无固定返利,卖出30件以内(含30件)的食品,每件食品商家返利5元,超出30件的部分每件返利8元.经统计,两个商家的试销情况茎叶图如下:
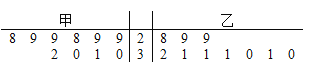
(1)现从甲商家试销的10天中抽取两天,求这两天的销售量都小于30的概率;
(2)若将频率视作概率,回答以下问题:
① 记商家乙的日返利额为X(单位:元),求X的分布列和数学期望;
② 超市拟在甲、乙两个商家中选择一家长期销售,如果仅从日平均返利额的角度考虑,请利用所学的统计学知识为超市作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年春节期间,某服装超市举办了一次有奖促销活动,消费每超过
年春节期间,某服装超市举办了一次有奖促销活动,消费每超过![]() 元(含
元(含![]() 元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.方案一:从装有
元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.方案一:从装有![]() 个形状、大小完全相同的小球(其中红球
个形状、大小完全相同的小球(其中红球![]() 个,黑球
个,黑球![]() 个)的抽奖盒中,一次性摸出
个)的抽奖盒中,一次性摸出![]() 个球,其中奖规则为:若摸到
个球,其中奖规则为:若摸到![]() 个红球,享受免单优惠;若摸出
个红球,享受免单优惠;若摸出![]() 个红球则打
个红球则打![]() 折,若摸出
折,若摸出![]() 个红球,则打
个红球,则打![]() 折;若没摸出红球,则不打折.方案二:从装有
折;若没摸出红球,则不打折.方案二:从装有![]() 个形状、大小完全相同的小球(其中红球
个形状、大小完全相同的小球(其中红球![]() 个,黑球
个,黑球![]() 个)的抽奖盒中,有放回每次摸取
个)的抽奖盒中,有放回每次摸取![]() 球,连摸
球,连摸![]() 次,每摸到
次,每摸到![]() 次红球,立减
次红球,立减![]() 元.
元.
(1)若两个顾客均分别消费了![]() 元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满![]() 元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com