
【题目】某校为了了解![]() 两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
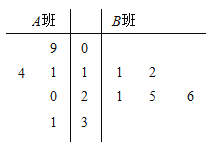
(1)分别求出图中所给两组样本数据的平均值,并据此估计哪个班的学生平均观看的时间较长;
(2)从![]() 班的样本数据中随机抽取一个不超过19的数据记为
班的样本数据中随机抽取一个不超过19的数据记为![]() ,从
,从![]() 班的样本数据中随机抽取一个不超过21的数据记为
班的样本数据中随机抽取一个不超过21的数据记为![]() ,求
,求![]() 的概率.
的概率.
【答案】(1)![]() 班学生平均观看时间较长;(2)
班学生平均观看时间较长;(2)![]() .
.
【解析】试题分析: (1)先根据平均数等于总数除以样本个数,计算两班平均值,再比较大小即可,(2)利用枚举法计算样本总数为9种,再从中计算满足![]() 的样本数,最后根据古典概型概率公式求概率.
的样本数,最后根据古典概型概率公式求概率.
试题解析:(1)![]() 班样本数据的平均值为
班样本数据的平均值为![]()
由此估计![]() 班学生平均观看时间大约为17小时,
班学生平均观看时间大约为17小时,
![]() 班样本数据的平均值为
班样本数据的平均值为![]() ,
,
由此估计![]() 班学生平均观看时间较长.
班学生平均观看时间较长.
(2)![]() 班的样本数据中不超过19的数据
班的样本数据中不超过19的数据![]() 有3个,分别为:9,11,14,
有3个,分别为:9,11,14,
![]() 班的样本数据中不超过21的数据
班的样本数据中不超过21的数据![]() 有3个,分别为:11,12,21,
有3个,分别为:11,12,21,
从![]() 班和
班和![]() 班的样本数据中各随机抽取一个共有9种不同情况,分别为:
班的样本数据中各随机抽取一个共有9种不同情况,分别为:![]()
其中![]() 的情况有
的情况有![]() 两种,
两种,
故![]() 的概率为
的概率为![]() .
.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】某市需对某环城快速车道进行限速,为了调研该道路车速情况,于某个时段随机对![]() 辆车的速度进行取样,测量的车速制成如下条形图:
辆车的速度进行取样,测量的车速制成如下条形图:
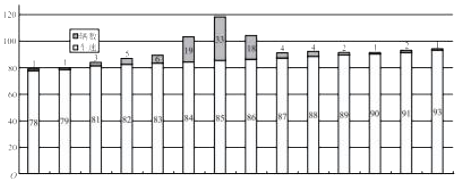
经计算:样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于
,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于![]() 或车速大于
或车速大于![]() 是需矫正速度.
是需矫正速度.
(1)从该快速车道上所有车辆中任取![]() 个,求该车辆是需矫正速度的概率;
个,求该车辆是需矫正速度的概率;
(2)从样本中任取![]() 个车辆,求这
个车辆,求这![]() 个车辆均是需矫正速度的概率;
个车辆均是需矫正速度的概率;
(3)从该快速车道上所有车辆中任取![]() 个,记其中是需矫正速度的个数为
个,记其中是需矫正速度的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,下图![]() 为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含
为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含![]() 个小正方形.
个小正方形.
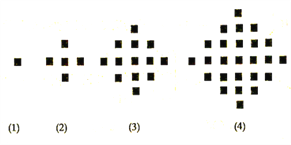
(1)求出![]() ;
;
(2)利用合情推理的“归纳推理思想”归纳出![]() 与
与![]() 的关系式,
的关系式,
(3)根据你得到的关系式求![]() 的表达式
的表达式
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品上市30天内每件的销售价格![]() 元与时间
元与时间![]() 天函数关系是
天函数关系是
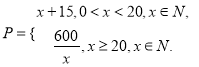 该商品的日销售量
该商品的日销售量![]() 件与时间
件与时间![]() 天函数关系是
天函数关系是
![]() .(1)求该商品上市第20天的日销售金额;
.(1)求该商品上市第20天的日销售金额;
(2)求这个商品的日销售金额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为常数,
为常数,![]() ).(Ⅰ)求函数
).(Ⅰ)求函数![]() 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立?如果存在,求
恒成立?如果存在,求![]() 的取值范围;如果不存在,请说明理由(其中
的取值范围;如果不存在,请说明理由(其中![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盐化某厂决定采用以下方式对某块盐池进行开采:每天开采的量比上一天减少![]() ,10天后总量变为原来的一半,为了维持生态平衡,剩余总量至少要保留原来的
,10天后总量变为原来的一半,为了维持生态平衡,剩余总量至少要保留原来的![]() ,已知到今天为止,剩余的总量是原来的
,已知到今天为止,剩余的总量是原来的![]() .
.
(1)求![]() 的值;
的值;
(2)到今天为止,工厂已经开采了几天?
(3)今后最多还能再开采多少天?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB的中点,且△PDB是正三角形,PA⊥PC.
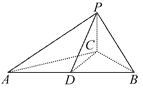
(1)求证:平面PAC⊥平面ABC.
(2)求二面角D-AP-C的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com