
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数)M是C1上的动点,P点满足
(α为参数)M是C1上的动点,P点满足 ![]() =2
=2 ![]() ,P点的轨迹为曲线C2
,P点的轨迹为曲线C2
(1)求C2的方程;
(2)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线θ= ![]() 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
【答案】
(1)解:设P(x,y),则由条件知M( ![]() ,
, ![]() ).由于M点在C1上,
).由于M点在C1上,
所以  即
即 ![]()
从而C2的参数方程为
![]() (α为参数)
(α为参数)
(2)解:曲线C1的极坐标方程为ρ=4sinθ,曲线C2的极坐标方程为ρ=8sinθ.
射线θ= ![]() 与C1的交点A的极径为ρ1=4sin
与C1的交点A的极径为ρ1=4sin ![]() ,
,
射线θ= ![]() 与C2的交点B的极径为ρ2=8sin
与C2的交点B的极径为ρ2=8sin ![]() .
.
所以|AB|=|ρ2﹣ρ1|= ![]()
【解析】(1)先设出点P的坐标,然后根据点P满足的条件代入曲线C1的方程即可求出曲线C2的方程;(2)根据(1)将求出曲线C1的极坐标方程,分别求出射线θ= ![]() 与C1的交点A的极径为ρ1 , 以及射线θ=
与C1的交点A的极径为ρ1 , 以及射线θ= ![]() 与C2的交点B的极径为ρ2 , 最后根据|AB|=|ρ2﹣ρ1|求出所求.
与C2的交点B的极径为ρ2 , 最后根据|AB|=|ρ2﹣ρ1|求出所求.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人进行某项对抗性游戏,采用“七局四胜”制,即先赢四局者为胜,若甲、乙两人水平相当,且已知甲先赢了前两局.
![]() Ⅰ
Ⅰ![]() 求乙取胜的概率;
求乙取胜的概率;
![]() Ⅱ
Ⅱ![]() 记比赛局数为X,求X的分布列及数学期望
记比赛局数为X,求X的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|ax﹣2|.
(1)若关于x的不等式f(x)<3的解集为(﹣ ![]() ,
, ![]() ),求a的值;
),求a的值;
(2)f(x)+f(﹣x)≥a对于任意x∈R恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+2﹣x .
(1)求方程f(x)= ![]() 的根;
的根;
(2)求证:f(x)在[0,+∞)上是增函数;
(3)若对于任意x∈[0,+∞),不等式f(2x)≥f(x)﹣m恒成立,求实数m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与平面ABCD所成角的正切值依次是1、![]() ,AP=2,E、F依次是PB、PC的中点.
,AP=2,E、F依次是PB、PC的中点.

(1)求证:PB⊥平面AEFD;
(2)求直线EC与平面PAD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在凸四边形ABCD中,AB=1,BC= ![]() ,AC⊥DC,CD=
,AC⊥DC,CD= ![]() AC.设∠ABC=θ.
AC.设∠ABC=θ. 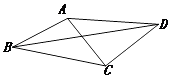
(1)若θ=30°,求AD的长;
(2)当θ变化时,求BD的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com