
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧(左)视图、俯视图,在直观图中, 是
是 的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
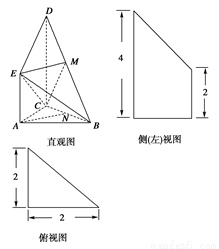
(1)求出该几何体的体积;
(2)若 是
是 的中点,求证:
的中点,求证: ∥平面
∥平面 ;
;
(3)求证:平面 ⊥平面
⊥平面 .
.
(1)4 (2)主要证明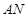 ∥
∥ (3)主要证明
(3)主要证明
 平面
平面
【解析】
试题分析:解:(1)由题意可知,四棱锥 中,
中,
平面
 平面
平面 ,
,

 ,
,
所以,
 平面
平面 ,
,
又 ,
,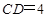 ,
,
则四棱锥 的体积为
的体积为
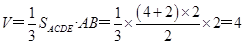 .
.
(2)连接 ,则
,则 ∥
∥ ,
,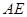 ∥
∥ ,
,
又 ,所以四边形
,所以四边形 为平行四边形,∴
为平行四边形,∴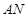 ∥
∥ ,
,
∵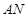
 平面
平面 ,
,
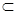 平面
平面 ,
,
所以,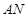 ∥平面
∥平面 .
.
(3)∵ ,
, 是
是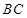 的中点,∴
的中点,∴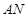 ⊥
⊥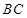 ,
,
又在直三棱柱中可知,平面
 平面
平面 ,
,
∴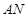
 平面
平面 ,
,
由(2)知,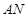 ∥
∥ ,∴
,∴
 平面
平面 ,
,
又
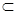 平面
平面 ,所以,平面
,所以,平面
 平面
平面 .
.
考点:平面与平面垂直的判定;棱柱、棱锥、棱台的体积;直线与平面平行的判定.
点评:本题考查的知识点是直线与平面平行的判定,棱锥的体积,平面与平面垂直的判定,其中(1)的关键是由面面垂直的性质定理可得AB⊥平面ACDE,(2)的关键是分析出四边形ANME为平行四边形,即AN∥EM,(3)的关键是熟练掌握空间线线垂直,线面垂直与面面垂直之间的相互转化.


科目:高中数学 来源: 题型:
 (2012•烟台三模)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(2012•烟台三模)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,M是BD的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,M是BD的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
(12分)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,![]() 是
是![]() 的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
![]() (Ⅰ)求出该几何体的体积;
(Ⅰ)求出该几何体的体积;
![]() (Ⅱ)求证:EM∥平面ABC;
(Ⅱ)求证:EM∥平面ABC;
![]() (Ⅲ) 试问在棱DC上是否存在点N,
(Ⅲ) 试问在棱DC上是否存在点N,
![]() 使NM⊥平面
使NM⊥平面![]() ? 若存在,确定点N的位置;
? 若存在,确定点N的位置;
![]() 若不存在,请说明理由.
若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,
![]() 是
是![]() 的中点.侧视图是直角梯形,俯视图是等腰直角
的中点.侧视图是直角梯形,俯视图是等腰直角
三角形,有关数据如图所示.
(Ⅰ)求出该几何体的体积;
(Ⅱ)求证:EM∥平面ABC;
(Ⅲ) 试问在棱DC上是否存在点N,使NM⊥平面![]() ? 若存在,确定点N的位置;
? 若存在,确定点N的位置;
若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三下学期二调考试文科数学试卷(解析版) 题型:解答题
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中, 是
是 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(Ⅰ)求出该几何体的体积。
(Ⅱ)若 是
是 的中点,求证:
的中点,求证: 平面
平面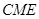 ;
;
(Ⅲ)求证:平面 平面
平面 .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com