


科目:高中数学 来源: 题型:
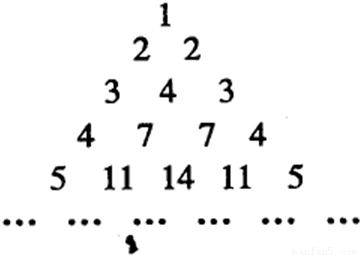
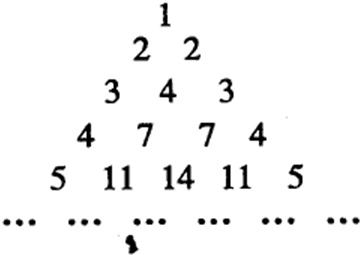 20、由部分自然数构成如图的数表,用aij(i≥j)表示第i行第j个数(i,j∈N*),使ai1=aii=i,每行中的其余各数分别等于其“肩膀”上的两个数的之和.设第n(n∈N*)行中各数之和为bn.
20、由部分自然数构成如图的数表,用aij(i≥j)表示第i行第j个数(i,j∈N*),使ai1=aii=i,每行中的其余各数分别等于其“肩膀”上的两个数的之和.设第n(n∈N*)行中各数之和为bn.查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)
由部分自然数构成如图的数表,用![]() 表示第
表示第![]() 行第
行第![]() 个数(
个数(![]() ),
),
使![]() ,每行中的其余各数分别等于其“肩膀”上的两个数的之和。设第
,每行中的其余各数分别等于其“肩膀”上的两个数的之和。设第
![]() 行中各数之和为
行中各数之和为![]() 。
。
(1)求![]() ;
;
(2)用![]() 表示
表示![]() ;
;
(3)试问:数列![]() 中是否存在不同的三项
中是否存在不同的三项![]() ,
,![]() ,
,![]() (
(![]() )恰好成等差数列?若存在,求出
)恰好成等差数列?若存在,求出![]() ,
,![]() ,
,![]() 的关系;若不存在,请说明理由。
的关系;若不存在,请说明理由。

查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)
由部分自然数构成如图的数表,用![]() 表示第
表示第![]() 行第
行第![]() 个数(
个数(![]() ),
),
使![]() ,每行中的其余各数分别等于其“肩膀”上的两个数的之和。设第
,每行中的其余各数分别等于其“肩膀”上的两个数的之和。设第
![]() 行中各数之和为
行中各数之和为![]() 。
。
(1)求![]() ;
;
(2)用![]() 表示
表示![]() ;
;
(3)试问:数列![]() 中是否存在不同的三项
中是否存在不同的三项![]() ,
,![]() ,
,![]() (
(![]() )恰好成等差数列?若存在,求出
)恰好成等差数列?若存在,求出![]() ,
,![]() ,
,![]() 的关系;若不存在,请说明理由。
的关系;若不存在,请说明理由。

查看答案和解析>>
科目:高中数学 来源:2010年广东省深圳市宝安中学高考数学考前热身训练试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com