
(1)①证明:两角和的余![]() 弦公式C(α+β):cos(α+β)=cos αcos β- sin αsin β;
弦公式C(α+β):cos(α+β)=cos αcos β- sin αsin β;
②由C(α+β)推导两角和的正弦公式S(α+β):sin(α+β![]() )=sin αcos β+cos αsinβ.
)=sin αcos β+cos αsinβ.
(2)已知△ABC的面积S=![]() ,
,![]() ·
·![]() =3,且cos B=
=3,且cos B=![]() ,求cos C.
,求cos C.
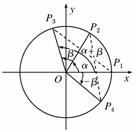
解![]() :(1)证明:①如图,在直角坐标系xOy内作单位圆O,
:(1)证明:①如图,在直角坐标系xOy内作单位圆O,![]() 并作出角α,β与-β,使角α的始边为Ox,交⊙O于点P1,终边交⊙O于点P2;角β的始边为OP2,终边交⊙O于点P3;角-β的始边为Ox,终边交⊙O于点P4,
并作出角α,β与-β,使角α的始边为Ox,交⊙O于点P1,终边交⊙O于点P2;角β的始边为OP2,终边交⊙O于点P3;角-β的始边为Ox,终边交⊙O于点P4,
则P1(1,0),P2(cos α,sin α),
P3(cos(α+β),sin(α+β)),
P4(cos(-β),sin(-β)).
由P1P3=P2P4及两点间的距离公式,得
[cos(α+β)-1]2+sin2(α+β)
=[cos(-β)-cos α]2+[sin(-β)-sin α]2,
展开整理,得2-2cos(α+β)=2-2(cos αcos β-sin αsin β).
∴cos(α+β)=cos αcos β-sin αsin β.
②由①易得,cos(![]() -α)=sin α,sin(
-α)=sin α,sin(![]() -α)=cos α.
-α)=cos α.
sin(α+β)=cos[![]() -(α+β)]=cos[(
-(α+β)]=cos[(![]() -α)+(-β)]
-α)+(-β)]
=cos(![]() -α)cos(-β)-sin(
-α)cos(-β)-sin(![]() -α)sin(-β)
-α)sin(-β)
=sin![]() αcos β+cos αsin β.∴sin(α+β)=sin αcos β+cos αsin β.
αcos β+cos αsin β.∴sin(α+β)=sin αcos β+cos αsin β.
(2)由题意,设△ABC的角B、C的对边分别为b、c,
则S=![]() bcsin A=
bcsin A=![]() ,即bcsin A=1.
,即bcsin A=1.
又![]() ·
·![]() =bc
=bc![]() cos A=3>0,∴A∈(0,
cos A=3>0,∴A∈(0,![]() ),cos A=3sin A.
),cos A=3sin A.
又sin2A+cos2A=1,∴sin A=![]() ,cos A=
,cos A=![]() .
.
由题知cos B=![]() ,得sin B=
,得sin B=![]() .
.
∴cos(A+B)=cos Acos B-sin Asin B=![]() .
.
∴cos C=cos[π-(A+B)]=-cos(A+![]() B)=-
B)=-![]() .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:阅读理解
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:阅读理解
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| AB |
| AC |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)①证明:两角和的余弦公式C(α+β):cos(α+β)=cos αcos β-sin αsin β;
②由C(α+β)推导两角和的正弦公式S(α+β):sin(α+β)=sin αcos β+cos αsin β.
(2)已知cos α=-![]() ,α∈(π,
,α∈(π,![]() π),
π),![]() tan β=-
tan β=-![]() ,β∈(
,β∈(![]() ,π),求cos(α+β).
,π),求cos(α+β).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com