
 ,且
,且 •
• =6,
=6, ,求
,求 的取值范围.
的取值范围. ,结合
,结合 得tanB∈[-1,-
得tanB∈[-1,- ],从而
],从而 ,再化简函数f(B)=2+
,再化简函数f(B)=2+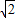 sin(2B+
sin(2B+ ),结合三角函数的图象与性质,可得函数f(B)的值域;
),结合三角函数的图象与性质,可得函数f(B)的值域; 、
、 都是单位向量,将
都是单位向量,将 平方化简得
平方化简得 =13-12sinB,结合角B的取值范围则不难得到
=13-12sinB,结合角B的取值范围则不难得到 的取值范围,进而可得到
的取值范围,进而可得到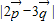 的取值范围.
的取值范围.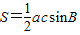 ,得2S=acsinB
,得2S=acsinB ,所以-6=accosB
,所以-6=accosB ,
,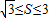 ,得
,得 ,
, …(2分).
…(2分).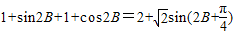 …(4分)
…(4分)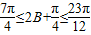 ,函数f(B)在区间[
,函数f(B)在区间[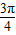 ,
, ]上为增函数
]上为增函数 时,函数有最小值为2+
时,函数有最小值为2+ sin
sin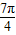 =1;当B=
=1;当B= 时,函数有最大值为2+
时,函数有最大值为2+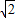 sin
sin =
=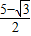
 …(6分).
…(6分). 可知:
可知: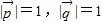 .…(8分).
.…(8分).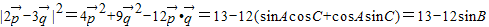 …(10分)
…(10分) ,∴sinB∈[
,∴sinB∈[ ,
, ]
]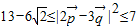 ,得到
,得到 …(12分).
…(12分).

科目:高中数学 来源: 题型:
| 3 |
| AB |
| BC |
| p |
| q |
| p |
| q |
查看答案和解析>>
科目:高中数学 来源:浙江省萧山中学2009届高三第一学期杭州地区七校联考数学试题 人教版 人教版 题型:044
已知△ABC的面积满足![]() ≤S≤3,且
≤S≤3,且![]() 的夹角为
的夹角为![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)求函数f(![]() )=sim2
)=sim2![]() +2sin
+2sin![]() cos
cos![]() +3cos2
+3cos2![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:吉林市江北区2010届高三第一次考试数学试卷(文科) 题型:044
已知△ABC的面积满足![]() ,且
,且![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)求函数f(![]() )=sin2
)=sin2![]() +2sin
+2sin![]() cos
cos![]() +3cos2
+3cos2![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省实验中学高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
 ,且
,且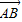 •
• =6,
=6, ,求
,求 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com