
 =(1-tanx,1),
=(1-tanx,1), =(1+sin2x+cos2x,0),记f(x)=
=(1+sin2x+cos2x,0),记f(x)= •
• .
.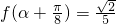 ,且
,且 ,求f(α).
,求f(α).解:(1)∵ =(1-tanx,1),
=(1-tanx,1), =(1+sin2x+cos2x,0),
=(1+sin2x+cos2x,0),
∴f(x)= •
• =(1-tanx)(1+sin2x+cos2x)
=(1-tanx)(1+sin2x+cos2x)
= =2(cos2x-sin2x)=2cos2x.
=2(cos2x-sin2x)=2cos2x.
定义域为 .
.
(2)因 ,即
,即 >0,
>0,
故 为锐角,于是
为锐角,于是 .
.
∴f(α)= =
= =
= .
.
 =(1-tanx,1),
=(1-tanx,1), =(1+sin2x+cos2x,0),求出f(x)=
=(1+sin2x+cos2x,0),求出f(x)= •
• ,化简为一个角的一个三角函数的形式,就是f(x)的解析式,指出它的定义域;
,化简为一个角的一个三角函数的形式,就是f(x)的解析式,指出它的定义域;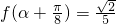 ,代入函数表达式,根据
,代入函数表达式,根据 ,求出
,求出 ,然后求f(α).
,然后求f(α). ”展开,并结合cos22α+sin22α=1,求解方程组,求cos2α的值.但三角恒等变换中,“三变”应加强必要的训练.
”展开,并结合cos22α+sin22α=1,求解方程组,求cos2α的值.但三角恒等变换中,“三变”应加强必要的训练. 

科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| c |
| 3 |
| c |
| a |
| b |
| a |
| b |
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| 2 |
| a |
| m |
| n |
| b |
| m |
| n |
| a |
| b |
| c |
| a |
| b |
| d |
| m |
| n |
| c |
| d |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| m |
| a |
| b |
| n |
| a |
| b |
| a |
| b |
| m |
| n |
| m |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com