
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() .
.
(1)直接写出函数![]() 的增区间(不需要证明);
的增区间(不需要证明);
(2)求出函数![]() ,
,![]() 的解析式;
的解析式;
(3)若函数![]() ,
,![]() ,求函数
,求函数![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)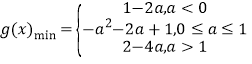 。
。
【解析】
(1)根据题意,由偶函数的性质结合二次函数的性质分析可得答案;
(2)设x>0,结合函数的奇偶性,从而得到函数的解析式;
(3)先求出g(x)的表达式,求出对称轴,通过讨论对称轴的位置,得到函数g(x)的最值
(1)根据题意,f(x)的增区间为(﹣1,0)、(1,+∞);
(2)根据题意,设x<0,则﹣x>0,
又由f(x)是定义在R上的偶函数,且当x≥0时,f(x)=x2﹣2x,
f(x)=f(﹣x)=x2+2x;
故函数的解析式为f(x)=![]() ;
;
(3)由(2)可得当x∈[1,2],f(x)=x2﹣2x,
则g(x)=f(x)﹣2ax+2=x2﹣2(a+1)x+2,
对称轴方程为:x=a+1,
①当a+1≤1时,g(x)min=g(1)=1﹣2a为最小;
②当1<a+1≤2时,g(x)min=g(a+1)=﹣a2﹣2a+1为最小;
③当a+1>2时,g(x)min=g(2)=2﹣4a为最小
故g(x)=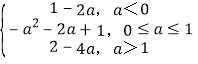 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx.
(1)求函数f(x)的图象在x=1处的切线方程;
(2)若函数y=f(x)+ ![]() 在[
在[ ![]() ,+∞)上有两个不同的零点,求实数k的取值范围;
,+∞)上有两个不同的零点,求实数k的取值范围;
(3)是否存在实数k,使得对任意的x∈( ![]() ,+∞),都有函数y=f(x)+
,+∞),都有函数y=f(x)+ ![]() 的图象在g(x)=
的图象在g(x)= ![]() 的图象的下方;若存在,请求出最大整数k的值,若不存在,请说明理由(参考数据:ln2=0.6931,
的图象的下方;若存在,请求出最大整数k的值,若不存在,请说明理由(参考数据:ln2=0.6931, ![]() =1.6487).
=1.6487).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(logax)= ![]() ,(0<a<1)
,(0<a<1)
(1)求f(x)的表达式,并判断f(x)的奇偶性;
(2)判断f(x)的单调性;
(3)对于f(x),当x∈(﹣1,1)时,恒有f(1﹣m)+f(1﹣m2)<0,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1的方程为x2+(y+1)2=4,圆C2的圆心坐标为(2,1).
(1)若圆C1与圆C2相交于A,B两点,且|AB|=![]() ,求点C1到直线AB的距离;
,求点C1到直线AB的距离;
(2)若圆C1与圆C2相内切,求圆C2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣mx(m∈R).
(1)若曲线y=f(x)过点P(1,﹣1),求曲线y=f(x)在点P的切线方程;
(2)若f(x)≤0恒成立求m的取值范围;
(3)求函数f(x)在区间[1,e]上最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量(百件)与销售单价x(元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.

(1)把y表示为x的函数;
(2)当销售价为每件50元时,该店正好收支平衡(即利润为零),求该店的职工人数;
(3)若该店只有20名职工,问销售单价定为多少元时,该专卖店可获得最大月利润?(注:利润=收入-支出)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人. 
(1)请补充完整频率分布直方图,并估计这组数据的平均数M;
(2)现根据初赛成绩从第四组和第六组中任意选2人,记他们的成绩分别为x,y.若|x﹣y|≥10,则称此二人为“黄金帮扶组”,试求选出的二人为“黄金帮扶组”的概率P1;
(3)以此样本的频率当作概率,现随机在这组样本中选出3名学生,求成绩不低于120分的人数ξ的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com