练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．北纬45°圈上有A，B两地，A在东经120°，B在西经150°，设地球的半径为R，则A、B两地的球面距离是$\frac{πR}{3}$．

    分析 由于甲、乙两地在同一纬度圈上，计算经度差，求出甲、乙两地对应的AB弦长，以及球心角，然后求出球面距离．

    解答 解：地球表面上从甲地（北纬45°，东经120°）到乙地（北纬45°，西经150°）
    甲、乙两地对应的AB的纬圆半径是$\frac{\sqrt{2}R}{2}$，经度差是90°，
    所以AB=R
    所以球心角是$\frac{π}{3}$，
    所以甲、乙两地的球面距离是$\frac{πR}{3}$．
    故答案为：$\frac{πR}{3}$．

    点评 本题考查球面距离及其他计算，考查空间想象能力，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．解方程：${C}_{25}^{2x}$=${C}_{25}^{x+4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．设a＜b，把函数y=h（x）的图象与直线x=a和x=b、y=0所围成的面积与b-a的比值称为函数y=h（x）在区间（a，b）上的“面积密度”．
    （1）设f（x）=x1n x-x，曲线y=f（x）与直线y=x+b相切，求b的值；
    （2）设0＜a≤b，求μ的值（用a，b表示）使得函数g（x）=|1n x-ln μ|在区间（a，b）上的“面积密度”取得最小值；
    （3）记（2）中的最小值为φ（a，b）求证φ（a，b）＜ln2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=xsinθ+cosθ，其中θ∈[0，2π）．
    （Ⅰ）若f（x）在（-∞，+∞）为减函数，求θ的取值范围；
    （Ⅱ）若函数f（x）为奇函数，求lnf（sinθ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．在△ABC中，BC=8，BC边上的高为6，则$\overrightarrow{AB}$•$\overrightarrow{AC}$的取值范围为[20，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知A、B是半径为R的球O的球面上两点，∠AOB=α，C为球面上的动点，若三棱锥O-ABC的体积最大，则α和最大体积分别为（　　）
    A．$\frac{π}{3}$，$\frac{1}{6}$R3B．$\frac{π}{3}$，$\frac{1}{3}$R3C．$\frac{π}{2}$，$\frac{1}{3}$R3D．$\frac{π}{2}$，$\frac{1}{6}$R3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

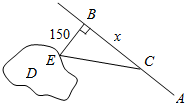    11．如图，一海岛D，海岛离岸边最近点B的距离是150km，在岸边距点B300km的点A处有一批物资需运往海岛D，为了尽快送达海岛，A与B之间有一铁路，现用海陆联运的方式，火车的时速为50km，船的时速为30km，试在岸边选一点C，问选在何处可使运输时间最短．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．函数y=x4+2x2-1的值域[-1，+∞）；函数y=$\frac{1}{{x}^{2}+1}$的值域（0，1]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．下列函数中，满足“f（xy）=f（x）+f（y）”的单调递减函数是（　　）
    A．f（x）=lnxB．f（x）=-x3C．f（x）=log${\;}_{\frac{1}{2}}$xD．f（x）=3-x

    查看答案和解析>>

    同步练习册答案