
(2006
山东,17)已知函数
 ,且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
,且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
(1)
求φ;(2)
计算f(1)+f(2)+…+f(2008).|
解析: (1)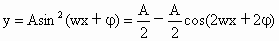 . .
∵ y=f(x)的最大值为2,A>0,∴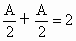 ,A=2. ,A=2.
又∵其图象相邻两对称轴间的距离为 2,w>0,∴  , ,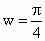 . .
∴  . .
∵ y=f(x)的图象过(1,2)点,∴ . .
∴  , ,
∴ 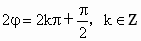 ,∴ ,∴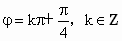 , ,
又∵  ∴ ∴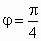 . .
(2) 解法一:∵ . .
∴  . .
∴ f(1)+f(2)+f(3)+f(4)=2+1+0+1=4.又∵ y=f(x)的周期为4,2008=4×502,∴ f(1)+f(2)+…+f(2008)=4×502=2008.解法二:∵ 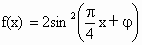 , ,
∴ 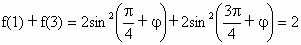 , ,
∴ f(1)+f(2)+f(3)+f(4)=4.又 y=f(x)的周期为4,2008=4×502.∴ f(1)+f(2)+…+f(2008)=4×502=2008. |
|
剖析:本题主要考查倍角公式、周期性、三角函数值的计算等综合知识. |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com