
【题目】已知![]() ,
,![]() ,直线AD与直线BD相交于点D,直线BD的斜率减去直线AD的斜率的差是2,设D点的轨迹为曲线C.
,直线AD与直线BD相交于点D,直线BD的斜率减去直线AD的斜率的差是2,设D点的轨迹为曲线C.
![]() 求曲线C的方程;
求曲线C的方程;
![]() 已知直线l过点
已知直线l过点![]() ,且与曲线C交于P,Q两点
,且与曲线C交于P,Q两点![]() Q异于A,
Q异于A,![]() ,问在y轴上是否存在定点G,使得
,问在y轴上是否存在定点G,使得![]() ?若存在,求出点G的坐标;若不存在,请说明理由.
?若存在,求出点G的坐标;若不存在,请说明理由.
科目:高中数学 来源: 题型:
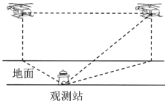
【题目】2019年10月1日,在庆祝新中国成立70周年阅兵中,由我国自主研制的军用飞机和军用无人机等参阅航空装备分秒不差飞越天安门,壮军威,振民心,令世人瞩目.飞行员高超的飞行技术离不开艰苦的训练和科学的数据分析.一次飞行训练中,地面观测站观测到一架参阅直升飞机以![]() 千米/小时的速度在同一高度向正东飞行,如图,第一次观测到该飞机在北偏西
千米/小时的速度在同一高度向正东飞行,如图,第一次观测到该飞机在北偏西![]() 的方向上,1分钟后第二次观测到该飞机在北偏东
的方向上,1分钟后第二次观测到该飞机在北偏东![]() 的方向上,仰角为
的方向上,仰角为![]() ,则直升机飞行的高度为________千米.(结果保留根号)
,则直升机飞行的高度为________千米.(结果保留根号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() (
(![]() ),数列
),数列![]() 满足
满足![]() (
(![]() ),且
),且![]()
(1)证明数列![]() 为等差数列,并求数列
为等差数列,并求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校举行“两城同创”的知识竞赛答题,高一年级共有1200名学生参加了这次竞赛.为了解竞赛成绩情况,从中抽取了100名学生的成绩进行统计.其中成绩分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示,请你解答下列问题:
,其频率分布直方图如图所示,请你解答下列问题:

(1)求![]() 的值;
的值;
(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人;
(3)根据频率分布直方图,估计这次平均分(用组中值代替各组数据的平均值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 的底面ABCD是边长为2的菱形,侧面PAD是正三角形,
的底面ABCD是边长为2的菱形,侧面PAD是正三角形,![]() ,E为AD的中点,二面角
,E为AD的中点,二面角![]() 为
为![]() .
.

![]() 证明:
证明:![]() 平面PBE;
平面PBE;
![]() 求点P到平面ABCD的距离;
求点P到平面ABCD的距离;
![]() 求直线BC与平面PAB所成角的正弦值.
求直线BC与平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近13年的宣传费
(单位:千元)的影响,对近13年的宣传费![]() 和年销售量
和年销售量![]()
![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

由散点图知,按![]() 建立
建立![]() 关于
关于![]() 的回归方程是合理的.令
的回归方程是合理的.令![]() ,则
,则![]() ,经计算得如下数据:
,经计算得如下数据:
|
|
|
|
|
|
10.15 | 109.94 | 0.16 | -2.10 | 0.21 | 21.22 |
(1)根据以上信息,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)已知这种产品的年利润![]() 与
与![]() 的关系为
的关系为![]() .根据(1)的结果,求当年宣传费
.根据(1)的结果,求当年宣传费![]() 时,年利润的预报值是多少?
时,年利润的预报值是多少?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且对任意的实数
,且对任意的实数![]() 都有
都有![]() (
(![]() 是自然对数的底数),且
是自然对数的底数),且![]() ,若关于
,若关于![]() 的不等式
的不等式![]() 的解集中恰有唯一一个整数,则实数
的解集中恰有唯一一个整数,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com