
分析 先根据条件求出函数的周期,然后根据周期进行化简得f(119.5)=f(-0.5),再根据奇偶性和条件将-0.5转化到区间[-3,-2]上,代入解析式可求出所求.
解答 解:∵偶函数f(x)对任意x∈R都有f(x)=-$\frac{1}{f(x-3)}$,且当x∈[-3,-2]时,f(x)=4x,
∴f(x+3)=-$\frac{1}{f(x)}$,∴f(x+6)=f(x),
即函数f(x)的周期为6,
∴f(119.5)=f(20×6-0.5)=f(-0.5)=-$\frac{1}{f(-0.5+3)}$=-$\frac{1}{f(2.5)}$,
又∵偶函数f(x),当x∈[-3,-2]时,有f(x)=4x,
∴f(119.5)=-$\frac{1}{f(2.5)}$=-$\frac{1}{f(-2.5)}$=-$\frac{1}{4×(-2.5)}$=$\frac{1}{10}$.
故答案为:$\frac{1}{10}$.
点评 本题主要考查了函数的奇偶性和周期性,要特别利用好题中有f(x)=-$\frac{1}{f(x-3)}$的关系式.在解题过程中,条件f(x+a)=-$\frac{1}{f(x)}$通常是告诉我们函数的周期为2a.属于中档题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:解答题
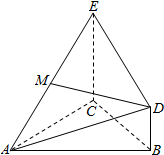 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE且CE=CA=2BD,M是EA的中点.
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE且CE=CA=2BD,M是EA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,E,F分别是CC1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,己知L、K分别是△ABC的边AB、AC的中点.△ABC的内切圆⊙l分别与边BC、CA切于点D、E.求证:KL、DE的交点在∠ABC的角平分线上.
如图,己知L、K分别是△ABC的边AB、AC的中点.△ABC的内切圆⊙l分别与边BC、CA切于点D、E.求证:KL、DE的交点在∠ABC的角平分线上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+1)2+(y-1)2=1 | B. | (x-1)2+(y+1)2=1 | ||
| C. | (x+1)2+(y+1)2=1 | D. | (x+1)2+(y-1)2=1或(x-1)2+(y+1)2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 7 | C. | 13 | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com