
【题目】给定椭圆C:![]() (
(![]() ),称圆心在原点O,半径为
),称圆心在原点O,半径为![]() 的圆是椭圆C的“卫星圆”.若椭圆C的离心率
的圆是椭圆C的“卫星圆”.若椭圆C的离心率![]() ,点
,点![]() 在C上.
在C上.
(1)求椭圆C的方程和其“卫星圆”方程;
(2)点P是椭圆C的“卫星圆”上的一个动点,过点P作直线![]() ,
,![]() 使得
使得![]()
![]()
![]() ,与椭圆C都只有一个交点,且
,与椭圆C都只有一个交点,且![]() ,
,![]() 分别交其“卫星圆”于点M,N,证明:弦长
分别交其“卫星圆”于点M,N,证明:弦长![]() 为定值.
为定值.
【答案】(1)![]() ,
,![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据题意列出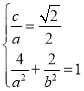 再结合
再结合![]() 即可解出
即可解出![]() ,
,![]() ,从而得到椭圆C的方程和其“卫星圆”方程;
,从而得到椭圆C的方程和其“卫星圆”方程;
(2) 根据![]()
![]()
![]() 分类讨论,当有一条直线斜率不存在时(不妨假设
分类讨论,当有一条直线斜率不存在时(不妨假设![]() 无斜率),可知其方程为
无斜率),可知其方程为![]() 或
或![]() ,这样可求出
,这样可求出![]() ;当两条直线的斜率都存在时,设经过点
;当两条直线的斜率都存在时,设经过点![]() 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为![]() ,与椭圆方程联立,由
,与椭圆方程联立,由![]() 可得
可得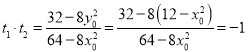 ,所以线段
,所以线段![]() 应为“卫星圆”的直径,即
应为“卫星圆”的直径,即![]() ,故得证.
,故得证.
(1)由条件可得: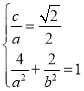
解得![]() ,
,![]()
所以椭圆的方程为![]() ,
,
卫星圆的方程为![]()
(2)①当![]() ,
,![]() 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设![]() 无斜率,
无斜率,
因为![]() 与椭圆只有一个公共点,则其方程为
与椭圆只有一个公共点,则其方程为![]() 或
或![]() ,
,
当![]() 方程为
方程为![]() 时,此时
时,此时![]() 与“卫星圆”交于点
与“卫星圆”交于点![]() 和
和![]() ,
,
此时经过点![]()
![]() 且与椭圆只有一个公共点的直线是
且与椭圆只有一个公共点的直线是
![]() 或
或![]() ,即
,即![]() 为
为![]() 或
或![]() ,
,
∴![]()
∴线段![]() 应为“卫星圆”的直径,
应为“卫星圆”的直径,
∴![]()
②当![]() ,
,![]() 都有斜率时,设点
都有斜率时,设点![]() ,其中
,其中![]() ,
,
设经过点![]() 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为![]() ,
,
则,
消去y得到![]() ,
,
∴![]()
∴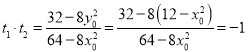
所以![]() ,满足条件的两直线
,满足条件的两直线![]() ,
,![]() 垂直.
垂直.
∴线段![]() 应为“卫星圆”的直径,∴
应为“卫星圆”的直径,∴![]()
综合①②知:因为![]() ,
,![]() 经过点
经过点![]() ,又分别交“卫星圆”于点
,又分别交“卫星圆”于点![]() ,且
,且![]() ,
,![]() 垂直,所以线段
垂直,所以线段![]() 是“卫星圆”
是“卫星圆”![]() 的直径,∴
的直径,∴![]() 为定值.
为定值.


科目:高中数学 来源: 题型:
【题目】函数![]() 的图象为C,如下结论中正确的是( )
的图象为C,如下结论中正确的是( )
①图象C关于直线![]() 对称;②函数
对称;②函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
③图象C关于点![]() 对称;④由
对称;④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象C
个单位长度可以得到图象C
A.①③B.②③C.①②③D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障人民群众的身体健康,在预防新型冠状病毒期间,贵阳市市场监督管理局加强了对市场的监管力度,对生产口罩的某工厂利用随机数表对生产的![]() 个口罩进行抽样测试是否合格,先将
个口罩进行抽样测试是否合格,先将![]() 个口罩进行编号,编号分别为
个口罩进行编号,编号分别为![]() ;从中抽取
;从中抽取![]() 个样本,如下提供随机数表的第
个样本,如下提供随机数表的第![]() 行到第
行到第![]() 行:
行:
![]()
![]()
![]()
若从表中第![]() 行第
行第![]() 列开始向右依次读取
列开始向右依次读取![]() 个数据,则得到的第
个数据,则得到的第![]() 个样本编号为( )
个样本编号为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三角形的边长为不相等的整数,且最大边长为n,这些三角形的个数为an.
(1)求数列{an}的通项公式;
(2)在1,2,…,100中任取三个不同的整数,求它们可以是一个三角形的三条边长的概率.
附:1+22+32+…+n2![]() ;1+23+33+…+n3
;1+23+33+…+n3![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
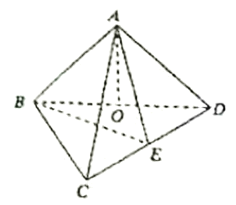
【题目】如图,在三棱锥![]() 中,顶点
中,顶点![]() 在底面
在底面![]() 上的射影
上的射影![]() 在棱
在棱![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点。
的中点。
(Ⅰ)求证:![]()
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)已知![]() 是平面
是平面![]() 内一点,点
内一点,点![]() 为
为![]() 中点,且
中点,且![]() 平面
平面![]() ,求线段
,求线段![]() 的长。
的长。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数,且
为常数,且![]() .
.
(1)若![]() 是奇函数,求
是奇函数,求![]() 的取值集合
的取值集合![]() ;
;
(2)当![]() 时,设
时,设![]() 的反函数
的反函数![]() ,且
,且![]() 的图象与
的图象与![]() 的图象关于
的图象关于![]() 对称,求
对称,求![]() 的取值集合
的取值集合![]() ;
;
(3)对于问题(1)(2)中的![]() 、
、![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com