
【题目】已知数列![]() 为等差数列,且
为等差数列,且![]() ,
,![]()
(Ⅰ)求数列![]() 的通项
的通项![]() ,及前
,及前![]() 项和
项和![]()
(Ⅱ)请你在数列![]() 的前4项中选出三项,组成公比的绝对值小于1的等比数列
的前4项中选出三项,组成公比的绝对值小于1的等比数列![]() 的前3项,并记数列
的前3项,并记数列![]() 的前n项和为
的前n项和为![]() .若对任意正整数
.若对任意正整数![]() ,不等式
,不等式![]() 恒成立,试求
恒成立,试求![]() 的最小值.
的最小值.
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】已知⊙M过点![]() ,且与⊙N:
,且与⊙N:![]() 内切,设⊙M的圆心M的轨迹为曲线C.
内切,设⊙M的圆心M的轨迹为曲线C.
(1)求曲线C的方程:
(2)设直线l不经过点![]() 且与曲线C相交于P,Q两点.若直线PB与直线QB的斜率之积为
且与曲线C相交于P,Q两点.若直线PB与直线QB的斜率之积为![]() ,判断直线l是否过定点,若过定点,求出此定点坐标;若不过定点,请说明理由.
,判断直线l是否过定点,若过定点,求出此定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆![]()
![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“准圆”.若椭圆
的“准圆”.若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上的一个端点到
,其短轴上的一个端点到![]() 的距离为
的距离为![]() .
.
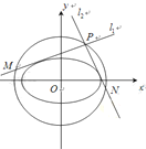
(1)求椭圆![]() 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点![]() 是椭圆
是椭圆![]() 的“准圆”上的动点,过点
的“准圆”上的动点,过点![]() 作椭圆的切线
作椭圆的切线![]() 交“准圆”于点
交“准圆”于点![]() .
.
①当点![]() 为“准圆”与
为“准圆”与![]() 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线![]() 的方程并证明
的方程并证明![]() ;
;
②求证:线段![]() 的长为定值.
的长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是一座具有划时代意义的大桥.它连通了珠海香港澳门三地,大大缩短了三地的时空距离,盘活了珠江三角洲的经济,被誉为新的世界七大奇迹.截至2019年10月23日8点,珠海公路口岸共验放出入境旅客超过1400万人次,日均客流量已经达到4万人次,验放出入境车辆超过70万辆次,2019年春节期间,客流再次大幅增长,日均客流达8万人次,单日客流量更是创下11.3万人次的最高纪录.
2019年从五月一日开始的连续100天客流量频率分布直方图如下
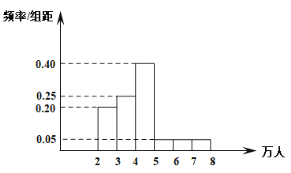
(1)①同一组数据用该区间的中点值代替,根据频率分布直方图.估计客流量的平均数.
②求客流量的中位数.
(2)设这100天中客流量超过5万人次的有![]() 天,从这
天,从这![]() 天中任取两天,设
天中任取两天,设![]() 为这两天中客流量超过7万人的天数.求
为这两天中客流量超过7万人的天数.求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),在极坐标系(与平面直角坐标系取相同的单位长度,以坐标原点
),在极坐标系(与平面直角坐标系取相同的单位长度,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴)中,曲线
轴正半轴为极轴)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() 可,试判断曲线
可,试判断曲线![]() 和
和![]() 的位置关系;
的位置关系;
(2)若曲线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 两点,且
两点,且![]() ,满足
,满足![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人进行抛硬币游戏,规定:每次抛币后,正面向上甲赢,否则乙赢.此时,两人正在游戏,且知甲再赢![]() (常数
(常数![]() )次就获胜,而乙要再赢
)次就获胜,而乙要再赢![]() (常数
(常数![]() )次才获胜,其中一人获胜游戏就结束.设再进行
)次才获胜,其中一人获胜游戏就结束.设再进行![]() 次抛币,游戏结束.
次抛币,游戏结束.
(1)若![]() ,
,![]() ,求概率
,求概率![]() ;
;
(2)若![]() ,求概率
,求概率![]() 的最大值(用
的最大值(用![]() 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为直角梯形![]() ,BC//A
,BC//A![]() ,
,![]() 为正三角形,M为PD中点.
为正三角形,M为PD中点.
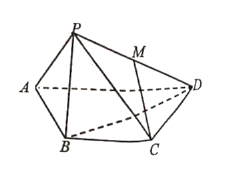
(1)证明:CM//平面PAB;
(2)若二面角P-AB-C的余弦值为![]() ,求直线AD与平面PBD所成角的正弦值.
,求直线AD与平面PBD所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com