
����Ŀ��ijѧУΪ�˽��У�����꼶ѧ����ѧ��ѧϰ�������һģ������ѧ�ɼ����з��������г�ȡ��![]() ��ѧ���ijɼ���Ϊ��������ͳ�ƣ���Уȫ��ѧ���ijɼ�����
��ѧ���ijɼ���Ϊ��������ͳ�ƣ���Уȫ��ѧ���ijɼ�����![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ķ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��1����ʾ�������з�����
�ķ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��1����ʾ�������з�����![]() �ڵ��������ݵľ�Ҷͼ��ͼ��2����ʾ�������ϼ�ͳ�ƻ���Ԥ¼�����ߣ������з�������ܱ�¼ȡԺУ��ζ��ձ�Ϊ����3����
�ڵ��������ݵľ�Ҷͼ��ͼ��2����ʾ�������ϼ�ͳ�ƻ���Ԥ¼�����ߣ������з�������ܱ�¼ȡԺУ��ζ��ձ�Ϊ����3����
���� |
|
|
|
���ܱ�¼ȡԺУ��� | ר�� | ���� | �ر� |
ͼ��3��
��1����![]() ��Ƶ�ʷֲ�ֱ��ͼ�е�
��Ƶ�ʷֲ�ֱ��ͼ�е�![]() ��
��![]() ��ֵ��
��ֵ��
��2�������������������˼�룬���¼�������Ƶ����Ϊ���ʣ����ڸ�У�����꼶ѧ������ȡ3�ˣ���������һ���ǿ���¼ȡΪ�ر����ԺУ�ĸ��ʣ�
��3����ѡȡ�������У��ӿ���¼ȡΪ�ر���ר��������ε�ѧ���������ȡ3��ѧ�����е��У��ñ�ʾ����ȡ��3��ѧ����Ϊ�ر������������������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
���𰸡���1��![]() ��
��![]() ��
��![]() ����2��
����2��![]() ��3���ֲ��м�������
��3���ֲ��м�������![]()
��������
��1����Ͼ�Ҷͼ�з�����70~80�������Լ�Ƶ�ʷֲ�ֱ��ͼ�ж�Ӧ��Ƶ�ʣ�����õ�n��x��y��ֵ��
��2�������ùŵ���ͼ���Ӹ�У�����꼶ѧ������ȡ1��Ϊ�ر��ĸ��ʣ���У�����꼶ѧ������ȡ3�ˣ�������һ���ܱ��ص��ѧ¼ȡ���¼����Ӷ���ֲ������ù�ʽ���㼴�ý⣻
��3���������![]() ���ӳ����ηֲ������ó����ηֲ��ĸ��ʹ�ʽ���㼴�ý�.
���ӳ����ηֲ������ó����ηֲ��ĸ��ʹ�ʽ���㼴�ý�.
�⣺��1���������֪����������![]() ��
��
���![]() ��
��![]() ��
��
��2���ɼ��ܱ��ص��ѧ¼ȡ������Ϊ![]() �ˣ�
�ˣ�
��ȡ��50���гɼ��ܱ��ص��ѧ¼ȡ��Ƶ����![]() ��
��
�ʴӸ�У�����꼶ѧ������ȡ1��Ϊ�ر��ĸ���Ϊ![]() ��
��
�Ǹ�У�����꼶ѧ������ȡ3�ˣ�������һ���ܱ��ص��ѧ¼ȡ���¼�Ϊ![]() ��
��
��![]() ��
��
��3���ɼ��ܱ��ص��ѧ¼ȡ������Ϊ15�ˣ��ɼ��ܱ�ר��ѧУ¼ȡ������![]() �ˣ����������
�ˣ����������![]() �����п���ȡֵΪ0��1��2��3��
�����п���ȡֵΪ0��1��2��3��
���ԣ�![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
���������![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
�������![]() ����ѧ����
����ѧ����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������װ��9ֻ�����б�������1��2��3��4��С���2����������5��С����1��.�Ӵ�����ȡ3��С��ÿ��С��ȡ���Ŀ����Զ���ȣ���![]() ��ʾȡ����3��С���ϵ��������.
��ʾȡ����3��С���ϵ��������.
��1����ȡ����3��С���ϵ����ֻ�����ͬ�ĸ��ʣ�
��2�����������![]() �ķֲ��к�����.
�ķֲ��к�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��.
��.
��1��������![]() �ڵ�
�ڵ�![]() �������߷���Ϊ
�������߷���Ϊ![]() ����a��ֵ��
����a��ֵ��
��2����![]() �Ǻ���
�Ǻ���![]() �ļ�ֵ�㣬��
�ļ�ֵ�㣬��![]() ����֤��
����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��������![]() ��ƽ���ı���
��ƽ���ı���![]() �;���
�;���![]() ��ɵ�һ��ƽ��ͼ�Σ�����
��ɵ�һ��ƽ��ͼ�Σ�����![]() ��
��![]() ��
��![]() ��
��![]() ��������
��������![]() ��
��![]() ����ʹ��
����ʹ��![]() ��
��![]() �غϣ���ͼ2��
�غϣ���ͼ2��

��1��֤����ͼ2�е�ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����ͼ2�е�![]() ��ƽ��
��ƽ��![]() �ľ��룻
�ľ��룻
��3����ͼ2�ж����![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ�������о���ѧϰ�У��Դ�����ҹ�²��С��ƶ����ӷ�ѿ����֮��Ĺ�ϵ�����о�����������4�·ݵ�30���������ѡ��5������о����ҷֱ��¼��ÿ����ҹ�²���ÿ��ÿ100�����ӽ��ݺ�ķ�ѿ�����õ��������ϣ�
���� | 4��1�� | 4��7�� | 4��15�� | 4��21�� | 4��30�� |
�²� | 10 | 11 | 13 | 12 | 8 |
��ѿ��y/�� | 23 | 25 | 30 | 26 | 16 |
��1������5������ѡ2�죬����2�췢ѿ������������С��25�ĸ��ʣ�
��2������5������ѡ2�죬��ѡȡ����4��1����4��30�յ��������ݣ��������5���е�����������ݣ����y����x�����Իع鷽��![]() ��
��
��3���������Իع鷽�̵õ��Ĺ�����������ѡ���ļ������ݵ�����������2�ţ�����Ϊ�õ������Իع鷽���ǿɿ��ģ����ʣ�2�������õ����Իع鷽���Ƿ�ɿ���
�����ع�ֱ�ߵ�б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ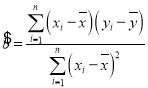 ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��1��31��������ȫʳ�Ĺ��̷�Ϊ������ʳ�ȡ�ʳ�������⡢��Բ����Σ���ʳ�ij���������19ʱ48�֣�20ʱ51��ʳ�ȣ�21ʱ29��ʳ����22ʱ07�����⣬23ʱ11�ָ�Բ.��ȫʳ�������������ͺ�������ȫʳ�ε�������������ʳ��ʱ�̿�ʼ������ʱ�̽���.С������19��55��21��56֮���ij��ʱ��������ȫʳ�������ȴ�������������ʱ�䲻����30���ӵĸ�����________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У�����
�У�����![]() Ϊ�������Σ�
��������![]() ��
��![]() ��
��![]() ��
��![]() �A����
�A����![]() .
.
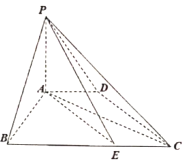
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��ƽ�潻
��ƽ�潻![]() �ڵ�
�ڵ�![]() ����ƽ��
����ƽ��![]() ������
������![]() �ֳ������ȵ������֣�������
�ֳ������ȵ������֣�������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com