
 .
.
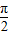 ))则△OHP的周长l=2+2cosα+2sinα,然后利用辅助角公式进行化简变形即可求出最大值,以及取最大值时点P的坐标.
))则△OHP的周长l=2+2cosα+2sinα,然后利用辅助角公式进行化简变形即可求出最大值,以及取最大值时点P的坐标.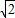
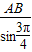 =
=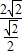 =4
=4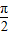 ))则
))则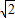 sin(α+
sin(α+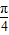 )
)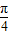 时,△OHP的周长l取最大值2+2
时,△OHP的周长l取最大值2+2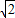 ,此时P(
,此时P(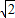 ,
,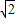 )
)

科目:高中数学 来源: 题型:
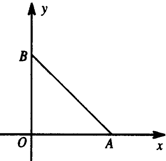 在如图所示的平面直角坐标系中,三角形AOB是腰长为2的等腰直角三角形,动点P与点O位于直线AB的两侧,且∠APB=
在如图所示的平面直角坐标系中,三角形AOB是腰长为2的等腰直角三角形,动点P与点O位于直线AB的两侧,且∠APB=| 3 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)=x2-2|x|-1.
已知函数f(x)=x2-2|x|-1.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(1≤t≤
(2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(1≤t≤| 3 |
| 2 |
| 9 |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
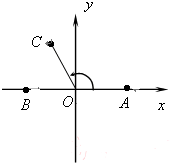 在如图所示的平面直角坐标系中,已知点.A(1,0)和点B(-1,0),|
在如图所示的平面直角坐标系中,已知点.A(1,0)和点B(-1,0),|| OC |
| 3 |
| 4 |
| OC |
| OD |
| π |
| 2 |
| m |
| BC |
| n |
| m |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com