
【题目】已知函数![]() 且
且![]() .
.
(I)若![]() ,求函数
,求函数![]() 的单调区间;(其中
的单调区间;(其中![]() 是自然对数的底数)
是自然对数的底数)
(II)设函数![]() ,当
,当![]() 时,曲线
时,曲线![]() 与
与![]() 有两个交点,求
有两个交点,求![]() 的取值范围.
的取值范围.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合 计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合 计 | 70 | 30 | 100 |
⑴根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差
异”;
⑵已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机
抽取3人,求至多有1人喜欢甜品的概率.
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
附: 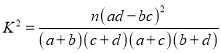 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,截至2016年底全国微信注册用户数量已经突破9.27亿.为调查大学生这个微信用户群体中每人拥有微信群的数量,现从某市大学生中随机抽取100位同学进行了抽样调查,结果如下:
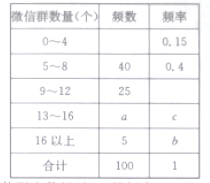
(1)求![]() ,
,![]() ,
,![]() 的值及样本中微信群个数超过12的概率;
的值及样本中微信群个数超过12的概率;
(2)若从这100位同学中随机抽取2人,求这2人中恰有1人微信群个数超过12的概率;
(3)以(1)中的频率作为概率,若从全市大学生中随机抽取3人,记![]() 表示抽到的是微信群个数超过12的人数,求
表示抽到的是微信群个数超过12的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为![]() .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.
(1)求某员工选择方案甲进行抽奖所获奖金![]() (元)的分布列;
(元)的分布列;
(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() 右焦点的直线
右焦点的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点, ![]() 为
为![]() 的中点,且直线
的中点,且直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设另一直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,原点
两点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,已知点
中,已知点![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为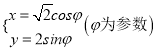 .以原点为极点,
.以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为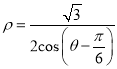 .
.
(Ⅰ)判断点![]() 与直线
与直线![]() 的位置关系并说明理由;
的位置关系并说明理由;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 的两个交点分别为
的两个交点分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
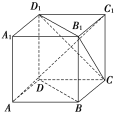
【题目】【2017唐山模拟】如图,ABCDA1B1C1D1为正方体,连接BD,AC1,B1D1, CD1,B1C,现有以下几个结论:①BD∥平面CB1D1;②AC1⊥平面CB1D1;③AC1与底面ABCD所成角的正切值是;④CB1与BD为异面直线,其中所有正确结论的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于下列命题: ①若函数y=2x的定义域是{x|x≤0},则它的值域是{y|y≤1};
②若函数y= ![]() 的定义域是{x|x>2},则它的值域是{y|y≤
的定义域是{x|x>2},则它的值域是{y|y≤ ![]() };
};
③若函数y=x2的值域是{y|0≤y≤4},则它的定义域一定是{x|﹣2≤x≤2};
④若函数y=log2x的值域是{y|y≤3},则它的定义域是{x|0<x≤8}.
其中不正确的命题的序号是 . (注:把你认为不正确的命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com