
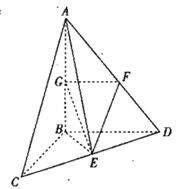
【题目】如图,三棱锥![]() 的三条侧棱两两垂直,
的三条侧棱两两垂直,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() 的中点.
的中点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某地级市共有200000中小学生,其中有7%学生在2017年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为5:3:2,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助1000元、1500元、2000元。经济学家调查发现,当地人均可支配年收入较上一年每增加![]() ,一般困难的学生中有
,一般困难的学生中有![]() 会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有
会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有![]() 转为一般困难,特别困难的学生中有
转为一般困难,特别困难的学生中有![]() 转为很困难。现统计了该地级市2013年到2017年共5年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份
转为很困难。现统计了该地级市2013年到2017年共5年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份![]() 取13时代表2013年,
取13时代表2013年, ![]() 与
与![]() (万元)近似满足关系式
(万元)近似满足关系式![]() ,其中
,其中![]() 为常数。(2013年至2019年该市中学生人数大致保持不变)
为常数。(2013年至2019年该市中学生人数大致保持不变)


其中![]() ,
, ![]()
(Ⅰ)估计该市2018年人均可支配年收入;
(Ⅱ)求该市2018年的“专项教育基金”的财政预算大约为多少?
附:对于一组具有线性相关关系的数据![]() ,其回归直线方程
,其回归直线方程 ![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,近日我渔船编队在岛![]() 周围海域作业,在岛
周围海域作业,在岛![]() 的南偏西20°方向有一个海面观测站
的南偏西20°方向有一个海面观测站![]() ,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与
,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与![]() 相距31海里的
相距31海里的![]() 处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛
处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛![]() 直线航行以保护我渔船编队,30分钟后到达
直线航行以保护我渔船编队,30分钟后到达![]() 处,此时观测站测得
处,此时观测站测得![]() 间的距离为21海里.
间的距离为21海里.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试问海警船再向前航行多少分钟方可到岛![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在直线l与曲线![]() 和曲线
和曲线![]() 都相切,则称曲线
都相切,则称曲线![]() 和曲线
和曲线![]() 为“相关曲线”,有下列四个命
为“相关曲线”,有下列四个命
题:
①有且只有两条直线l使得曲线![]() 和曲线
和曲线![]() 为“相关曲线”;
为“相关曲线”;
②曲线![]() 和曲线
和曲线![]() 是“相关曲线”;
是“相关曲线”;
③当![]() 时,曲线
时,曲线![]() 和曲线
和曲线![]() 一定不是“相关曲线”;
一定不是“相关曲线”;
④必存在正数![]() 使得曲线
使得曲线![]()
![]() 和曲线
和曲线![]()
![]() 为“相关曲线”.
为“相关曲线”.
其中正确命题的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与平面
与平面![]() ,
,![]() ,下列命题:
,下列命题:
①若![]() 平行
平行![]() 内的一条直线,则
内的一条直线,则![]() ;②若
;②若![]() 垂直
垂直![]() 内的两条直线,则
内的两条直线,则![]() ;③若
;③若![]() 且
且![]() ,则
,则![]() ;④若mα,lβ且
;④若mα,lβ且![]() ,则
,则![]() ;⑤若
;⑤若![]() ,且
,且![]() ,则
,则![]() ;⑥若
;⑥若![]() ,
,![]() ,
,![]() ,则
,则![]() ;其中正确的命题为______________(填写所有正确命题的编号).
;其中正确的命题为______________(填写所有正确命题的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 命题“若x2-4x+3=0,则x=3”的逆否命题是:“若x≠3,则x2-4x+3≠0”
B. “x>1”是“|x|>0”的充分不必要条件
C. 若p且q为假命题,则p、q均为假命题
D. 命题p:“x0∈R使得![]() +x0+1<0”,则
+x0+1<0”,则![]() p:“x∈R,均有x2+x+1≥0”
p:“x∈R,均有x2+x+1≥0”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com