
分析 (1)求出A,B,C的坐标,即可求$\frac{{|{BC}|}}{{|{AC}|}}$的值;
(2)直线l的方程为y=k(x-1),若|BC|=2|AC|,则|xB-xC|=2|xA-xC|,求出k,即可求直线l的方程.
解答 解:(1)直线l的方程为y=3(x-1).
令y=0,得A(1,0).…(1分),令x=0,得B(0,-3).…(2分)
由$\left\{\begin{array}{l}y=x\\ y=3({x-1})\end{array}\right.$得${x_C}=\frac{3}{2}$…(3分)
$\frac{{|{BC}|}}{{|{AC}|}}=\frac{{|{{x_B}-{x_C}}|}}{{|{{x_A}-{x_C}}|}}=\frac{{|{\frac{3}{2}}|}}{{|{\frac{1}{2}}|}}=3$…(5分)
(2)直线l的方程为y=k(x-1).
令y=0,得A(1,0).令x=0,得B(0,-k).…(6分)
由$\left\{\begin{array}{l}y=x\\ y=k({x-1})\end{array}\right.$得${x_C}=\frac{k}{k-1}$…(7分)
若|BC|=2|AC|,则|xB-xC|=2|xA-xC|…(8分)
∴$|{\frac{k}{k-1}}|=2|{1-\frac{k}{k-1}}|$…(9分)
∴解得k=±2…(11分)
∴所求直线l的方程为:2x-y-2=0或2x+y-2=0.…(12分)
点评 本题考查直线方程,考查直线与直线位置关系的运用,考查学生的计算能力,属于中档题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
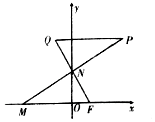 已知点F(1,0),动点M,N分别在x轴,y轴上运动,MN⊥NF,Q为平面上一点,$\overrightarrow{NQ}+\overrightarrow{NF}=\overrightarrow 0$,过点Q作QP平行于x轴交MN的延长线于点P.
已知点F(1,0),动点M,N分别在x轴,y轴上运动,MN⊥NF,Q为平面上一点,$\overrightarrow{NQ}+\overrightarrow{NF}=\overrightarrow 0$,过点Q作QP平行于x轴交MN的延长线于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 20 | C. | 35 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 都不大于2 | B. | 都不小于2 | ||
| C. | 至少有一个不大于2 | D. | 至少有一个不小于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | b<a<c | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com