
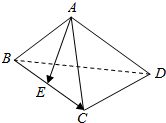
| A. | $\overrightarrow{AE}•\overrightarrow{BC}$<$\overrightarrow{AE}•\overrightarrow{CD}$ | B. | $\overrightarrow{AE}•\overrightarrow{BC}$=$\overrightarrow{AE}•\overrightarrow{CD}$ | ||
| C. | $\overrightarrow{AE}•\overrightarrow{BC}$>$\overrightarrow{AE}•\overrightarrow{CD}$ | D. | $\overrightarrow{AE}•\overrightarrow{BC}$与$\overrightarrow{AE}•\overrightarrow{CD}$大小不确定 |
分析 空间四边形ABCD的各条边的长度相等,不妨取为1,E为BC中点,可得:AE⊥BC,AB⊥CD,$\overrightarrow{AE}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$.代入计算即可得出.
解答 解:∵空间四边形ABCD的各条边的长度相等,不妨取为1,E为BC中点,
∴AE⊥BC,AB⊥CD,$\overrightarrow{AE}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$.
∴$\overrightarrow{AE}•\overrightarrow{BC}$=0,
$\overrightarrow{AE}$$•\overrightarrow{CD}$=$\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$$•\overrightarrow{CD}$
=$\frac{1}{2}\overrightarrow{AC}•\overrightarrow{CD}$
=$\frac{1}{2}×1×1×cos12{0}^{°}$=-$\frac{1}{4}$.
∴$\overrightarrow{AE}•\overrightarrow{BC}$$>\overrightarrow{AE}•\overrightarrow{CD}$.
故选:C.
点评 本题考查了正四面体的性质、数量积的运算性质、向量的平行四边形法则,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
 甲、乙两药厂生产同一型号药品,在某次质量检测中,两厂各有5份样品送检,检测的平均得分相等(检测满分为100分,得分高低反映该样品综合质量的高低).成绩统计用茎叶图表示如下:则a=3.
甲、乙两药厂生产同一型号药品,在某次质量检测中,两厂各有5份样品送检,检测的平均得分相等(检测满分为100分,得分高低反映该样品综合质量的高低).成绩统计用茎叶图表示如下:则a=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com