
已知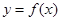 的定义域为
的定义域为 ,且恒有等式
,且恒有等式 对任意的实
对任意的实
数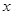 成立.
成立.
(Ⅰ)试求 的解析式;
的解析式;
(Ⅱ)讨论 在
在 上的单调性,并用单调性定义予以证明.
上的单调性,并用单调性定义予以证明.
(Ⅰ)f(x)=[2^(-x)-2^(x+1)]/3
(Ⅱ)函数在R上为减函数,证明见解析。
【解析】本试题主要是考查了求解函数的解析式,以及函数单调性的证明。
(1)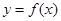 的定义域为
的定义域为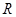 ,且恒有等式
,且恒有等式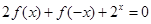 对任意的实数
对任意的实数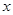 成立.,那么可以得到方程组,消元法得到结论。
成立.,那么可以得到方程组,消元法得到结论。
(2)设出变量,运用定义法证明单调性。
解:
1、2f(x)+f(-x)+2^x=0 …………1
2f(-x)+f(x)+2^(-x)=0 …………2
1式X2-2式得:
3f(x)+2^(x+1)-2^(-x)=0
即:f(x)=[2^(-x)-2^(x+1)]/3
2、设x1<x2 可得:
f(x1)-f(x2)
=[2^(-x1)-2^(x1+1)]/3-[2^(-x2)-2^(x2+1)]/3
=[2^(-x1)-2^(-x2)]/3+[2^(x2+1)-2^(x1+1)]/3
因:x1<x2 所以有:-x1>-x2 ,x1+1<x2+1
所以:2^(-x1)>2^(-x2)
2^(x2+1)>2^(x1+1)
即:f(x1)-f(x2)>0
所以此函数在R上为减函数!


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2015届贵州省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数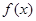 定义域为
定义域为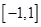 ,若对于任意的
,若对于任意的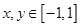 ,都有
,都有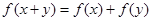 ,且
,且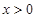 时,有
时,有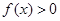 .
.
(1)求证: 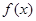 为奇函数;
为奇函数;
(2)求证: 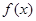 在
在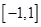 上为单调递增函数;
上为单调递增函数;
(3)设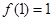 ,若
,若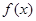 <
<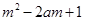 ,对所有
,对所有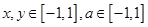 恒成立,求实数
恒成立,求实数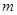 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高一元月文理分班考试数学 题型:解答题
(13分,理科做)已知函数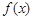 的定义域为
的定义域为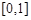 ,且同时满足:①
,且同时满足:①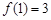 ;②
;②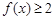 恒成立;③若
恒成立;③若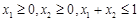 ,则有
,则有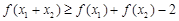 .
.
(1)试求函数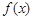 的最大值和最小值;
的最大值和最小值;
(2)试比较 与
与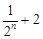 的大小
的大小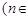 N);
N);
(3)某人发现:当x= (nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1
(nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1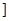 ,都有
,都有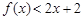 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com