分析:(1)欲求直线 A1C与平面ABCD所成角的正弦的值,在正方体ABCD-A1B1C1D1中,由于AC为A1C在平面ABCD的射影,故∠A1CA为A1C与平面ABCD所成角,最后在直角三角形中求解即得;
(2)欲证平面AB1D1∥平面EFG,根据面面平行的判定定理可知,只须证明线面平行即可.在正方体ABCD-A1B1C1D1中连接BD,则DD1∥BB1,DD1=BB1,利用直线间的平行关系可证得:D1B1∥平面GEF及AB1∥平面GEF,从而问题解决.
解答: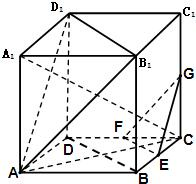
解:(1)∵A
1C∩平面ABCD=C,在正方体ABCD-A
1B
1C
1D
1中A
1A⊥平面ABCD
∴AC为A
1C在平面ABCD的射影
∴∠A
1CA为A
1C与平面ABCD所成角
sinA1CA==正方体的棱长为a∴AC=
a,A
1C=
a证明:(2)在正方体ABCD-A
1B
1C
1D
1中
连接BD,则DD
1∥BB
1,DD
1=BB
1,
∴D
1DBB
1为平行四边形
∴D
1B
1∥DB
∵E,F分别为BC,CD的中点
∴EF∥BD∴EF∥D
1B
1∵EF?平面GEF,D
1B
1?平面GEF
∴D
1B
1∥平面GEF
同理AB
1∥平面GEF
∵D
1B
1∩AB
1=B
1∴平面AB
1D
1∥平面EFG.
点评:本题主要考查了直线与平面之间所成角、平面与平面平行的判定、平面与平面垂直的判定,考查空间想象能力、运算能力和推理论证能力,属于中档题.

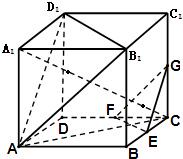 如图,在棱长为ɑ 的正方体ABCD-A1B1C1D1中,E、F、G分别是CB.CD.CC1的中点.
如图,在棱长为ɑ 的正方体ABCD-A1B1C1D1中,E、F、G分别是CB.CD.CC1的中点. 解:(1)∵A1C∩平面ABCD=C,在正方体ABCD-A1B1C1D1中A1A⊥平面ABCD
解:(1)∵A1C∩平面ABCD=C,在正方体ABCD-A1B1C1D1中A1A⊥平面ABCD

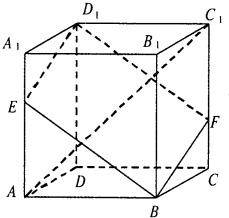 如图,在棱长为3的正方体ABCD-A1B1C1D1中,A1E=CF=1.
如图,在棱长为3的正方体ABCD-A1B1C1D1中,A1E=CF=1.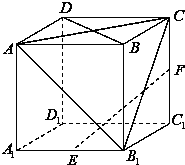 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是A1B1和CC1的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是A1B1和CC1的中点.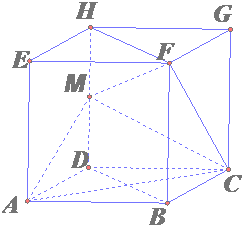
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,C1D1的中点,G是侧面BCC1B1的中心,则空间四边形AEFG在正方体的六个面上的射影图形面积的最大值是( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,C1D1的中点,G是侧面BCC1B1的中心,则空间四边形AEFG在正方体的六个面上的射影图形面积的最大值是( )