
【题目】选修4-5:不等式选讲
已知函数f(x)=|2x+1|+|2x-a|.
(I)若f(x)的最小值为2,求a的值;
(II)若f(x)≤|2x-4|的解集包含[-2,-1],求a的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由绝对值三角不等式可得函数f(x)的最小值为|a+1|,再解方程|a+1|=2,可得a的值;(2)即x∈[﹣2,﹣1]时,f(x)≤|2x﹣4|恒成立,化简得|2x﹣a|≤5恒成立,即﹣5+2x≤a≤5+2x恒成立,可得a的取值范围.
试题解析:解:(1)∵函数f(x)=|2x+1|+|2x﹣a|≥|2x+1﹣(2x﹣a)|=|a+1|,且f(x)的最小值为2,∴|a+1|=2,∴a=1 或a=﹣3.
(2)f(x)≤|2x﹣4|的解集包含[﹣2,﹣1],即x∈[﹣2,﹣1]时,f(x)≤|2x﹣4|恒成立,
即|2x+1|+|2x﹣a|≤|2x﹣4|恒成立,即﹣2x﹣1+|2x﹣a|≤4﹣2x恒成立,
即|2x﹣a|≤5恒成立,即﹣5+a≤2x≤5+a恒成立,即![]() ,
,
∴﹣7≤a≤1


科目:高中数学 来源: 题型:
【题目】已知在△ABC中,三条边![]() 所对的角分别为A、B,C,向量
所对的角分别为A、B,C,向量![]() =(
=(![]() ),
),![]() =(
=(![]() ),且满足
),且满足![]()
![]() =
=![]() .
.
(1)求角C的大小;
(2)若sinA,sinC,sinB成等比数列,且![]() =﹣8,求边
=﹣8,求边![]() 的值并求△ABC外接圆的面积.
的值并求△ABC外接圆的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,圆
轴的正半轴重合,圆![]() 的极坐标方程是
的极坐标方程是![]() ,直线
,直线![]() 的参数方程是
的参数方程是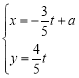 (
(![]() 为参数).
为参数).
(1)若![]() ,
,![]() 为直线
为直线![]() 与
与![]() 轴的交点,
轴的交点,![]() 是圆
是圆![]() 上一动点,求
上一动点,求![]() 的最大值;
的最大值;
(2)若直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥DC,AE⊥DC,BE∥AD.M、N分别是AD、BE上的点,且AM=BN,将三角形ADE沿AE折起,则下列说法正确的是 (填上所有正确说法的序号).
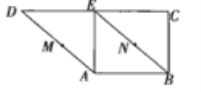
①不论D折至何位置(不在平面ABC内)都有MN∥平面DEC;
②不论D折至何位置都有MN⊥AE;
③不论D折至何位置(不在平面ABC内)都有MN∥AB;
④在折起过程中,一定存在某个位置,使EC⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为![]() ,据此解答如下问题.
,据此解答如下问题.
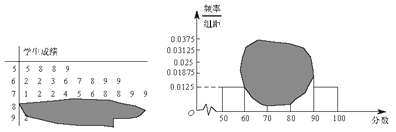
(Ⅰ)求全班人数及分数在![]() 之间的频率;
之间的频率;
(Ⅱ)现从分数在![]() 之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在
之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在![]() 的份数为
的份数为![]() ,求
,求![]() 的分布列和数学望期.
的分布列和数学望期.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的方程为
处的切线的方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的点80%,求![]() 的值;
的值;

(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com