
(本小题满分13分)已知函数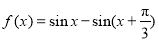 .
.
(1)求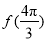 的值;
的值;
(2)求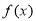 的单调递增区间.
的单调递增区间.
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知定义在正实数集上的函数f(x)=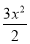 +ax,g(x)=4a2lnx+b,其中a>0,设两曲线y=f(x)与y=g(x)有公共点,且在公共点处的切线相同.
+ax,g(x)=4a2lnx+b,其中a>0,设两曲线y=f(x)与y=g(x)有公共点,且在公共点处的切线相同.
(1)若a=1,求两曲线y=f(x)与y=g(x)在公共点处的切线方程;
(2)用a表示b,并求b的最大值.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试文科数学试卷(解析版) 题型:选择题
已知曲线  在点 P(1,4)处的切线与直线 l 平行且距离为
在点 P(1,4)处的切线与直线 l 平行且距离为 ,则直线 l 的方程为( )
,则直线 l 的方程为( )
A. 或
或
B.
C. 或
或
D.以上都不对
查看答案和解析>>
科目:高中数学 来源:2015届北京市海淀区高三上学期期中练习文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知函数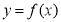 ,
,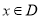 ,设曲线
,设曲线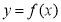 在点
在点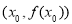 处的切线方程为
处的切线方程为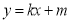 . 如果对任意的
. 如果对任意的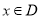 ,均有:
,均有:
①当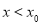 时,
时,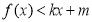 ;
;
②当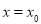 时,
时, ;
;
③当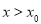 时,
时,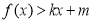 ,
,
则称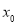 为函数
为函数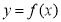 的一个“? -点”.
的一个“? -点”.
(1)判断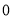 是否是下列函数的“? -点”:
是否是下列函数的“? -点”:
①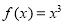 ; ②
; ②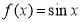 .(只需写出结论)
.(只需写出结论)
(2)设函数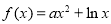 .
.
(ⅰ)若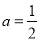 ,证明:
,证明: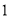 是函数
是函数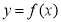 的一个“? -点”;
的一个“? -点”;
(ⅱ)若函数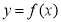 存在“? -点”,直接写出
存在“? -点”,直接写出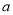 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三统一质量检测考试理科数学试卷(解析版) 题型:选择题
已知集合M={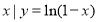 },集合N={
},集合N={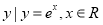 },(e为自然对数的底数)则
},(e为自然对数的底数)则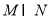 =( )
=( )
A.{ } B.{
} B.{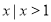 } C.{
} C.{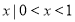 } D.
} D.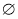
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com