
【题目】如图所示,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
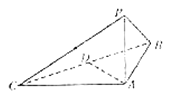
(1)求证:![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由余弦定理求出BC,因为![]() 为
为![]() 的中点,得BD=CD,因为
的中点,得BD=CD,因为![]() ,平方求出AD,利用勾股定理得AB⊥AD,结合PA⊥AD,得AD⊥平面PAB,从而AD⊥PB得证.
,平方求出AD,利用勾股定理得AB⊥AD,结合PA⊥AD,得AD⊥平面PAB,从而AD⊥PB得证.
(2)分别以直线AB,AD,AP为x轴,y轴,z轴建立空间直角坐标系,设PA=a,求出平面PBC的法向量,平面PAB的法向量,利用向量法求出a,然后求解VP﹣ABC=![]() ×S△ABC×PA即可.
×S△ABC×PA即可.
(1)在![]() 中,由余弦定理得
中,由余弦定理得![]() ,则
,则![]() .
.
因为![]() 为
为![]() 的中点,则
的中点,则![]() .
.
因为![]() ,则
,则![]()
![]() ,所以
,所以![]() .
.
因为![]() ,则
,则![]() .
.
因为![]() 底面
底面![]() ,则
,则![]() ,所以
,所以![]() 平面
平面![]() ,从而
,从而![]() .
.
(2)分别以直线![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,如图所示.
轴建立空间直角坐标系,如图所示.

设![]() ,则点
,则点![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,即
,即![]() ,
,
取![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() .
.
因为![]() 为平面
为平面![]() 的法向量,
的法向量,
则![]() ,即
,即![]() .
.
所以 ,解得
,解得![]() ,所以
,所以![]() .
.
所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】网约车的兴起丰富了民众出行的选择,为民众出行提供便利的同时也解决了很多劳动力的就业问题,据某著名网约车公司“滴滴打车”官网显示,截止目前,该公司已经累计解决退伍军人转业为兼职或专职司机三百多万人次,梁某即为此类网约车司机,据梁某自己统计某一天出车一次的总路程数可能的取值是20、22、24、26、28、![]() ,它们出现的概率依次是
,它们出现的概率依次是![]() 、
、![]() 、
、![]() 、
、![]() 、t、
、t、![]() .
.
(1)求这一天中梁某一次行驶路程X的分布列,并求X的均值和方差;
(2)网约车计费细则如下:起步价为5元,行驶路程不超过![]() 时,租车费为5元,若行驶路程超过
时,租车费为5元,若行驶路程超过![]() ,则按每超出
,则按每超出![]() (不足
(不足![]() 也按
也按![]() 计程)收费3元计费.依据以上条件,计算梁某一天中出车一次收入的均值和方差.
计程)收费3元计费.依据以上条件,计算梁某一天中出车一次收入的均值和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米.

(1)现在准备养一批供游客观赏的鱼,分别在AB、BC、CA上取点D,E,F,如图(1),使得EF‖AB,EF⊥ED,在△DEF喂食,求△DEF 面积S△DEF的最大值;
(2)现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,如图(2),建造△DEF
连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,求△DEF边长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求证:椭圆![]() 中斜率为
中斜率为![]() 的平行弦的中点轨迹必过椭圆中心;
的平行弦的中点轨迹必过椭圆中心;
(2)用作图方法找出下面给定椭圆的中心;
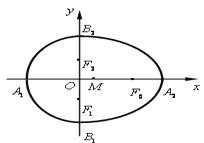
(3)我们把由半椭圆![]()
![]() 与半椭圆
与半椭圆![]()
![]() 合成的曲线称作“果圆”,其中
合成的曲线称作“果圆”,其中![]() ,
,![]() ,
,![]() .如图,设点
.如图,设点![]() ,
,![]() ,
,![]() 是相应椭圆的焦点,
是相应椭圆的焦点,![]() ,
,![]() 和
和![]() ,
,![]() 是“果圆” 与
是“果圆” 与![]() ,
,![]() 轴的交点. 连结“果圆”上任意两点的线段称为“果圆”的弦.试研究:是否存在实数
轴的交点. 连结“果圆”上任意两点的线段称为“果圆”的弦.试研究:是否存在实数![]() ,使斜率为
,使斜率为![]() 的“果圆”平行弦的中点轨迹总是落在某个椭圆上?若存在,求出所有可能的
的“果圆”平行弦的中点轨迹总是落在某个椭圆上?若存在,求出所有可能的![]() 值,若不存在,说明理由.
值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,A(0,1),AB边上的高CD所在直线的方程为x+2y-4=0,AC边上的中线BE所在直线的方程为2x+y-3=0.
(1)求直线AB的方程;
(2)求直线BC的方程;
(3)求△BDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com