
分析 (1)设点P(x,y),根据题意有 4$\sqrt{{(x+2)}^{2}{+y}^{2}}$+4(x-2)=0,整理得点P的轨迹C的方程.
(2)设S(x1,y1),T(x2,y2),把ST的方程与y2=-8x联立消元,利用韦达定理以及判别式大于零,求得-1<k<0.求得线段ST中点B的坐标为(-$\frac{4}{{k}^{2}}$+2,-$\frac{4}{k}$),可得线段ST的垂直平分线方程为y+$\frac{4}{k}$=-$\frac{1}{k}$(x+$\frac{4}{{k}^{2}}$-2).令y=0得点Q横坐标为xQ=-2-$\frac{4}{{k}^{2}}$<-6,即为Q点横坐标的取值范围.
解答 解:(1)设点P(x,y),根据题意则有:
$\overrightarrow{MN}$=(4,0),|$\overrightarrow{MN}$|=4,|$\overrightarrow{MP}$|=$\sqrt{{(x+2)}^{2}{+y}^{2}}$,$\overrightarrow{NP}$=(x-2,y),
代入|$\overrightarrow{MN}$||$\overrightarrow{MP}$|+$\overrightarrow{MN}$•$\overrightarrow{NP}$=0,得:4$\sqrt{{(x+2)}^{2}{+y}^{2}}$+4(x-2)=0.
整理得点P的轨迹C的方程:y2=-8x.
(2)设S(x1,y1),T(x2,y2),由题意得:ST的方程为y=k(x-2)(显然k≠0),
与y2=-8x联立消元得:ky2+8y+16k=0,则有:y1+y2=-$\frac{8}{k}$,y1•y2=16.
因为直线交轨迹C于两点,△=b2-4ac=64-64k2>0,
再由y1>0,y2>0,则-$\frac{8}{k}$>0,故-1<k<0.
可求得线段ST中点B的坐标为(-$\frac{4}{{k}^{2}}$+2,-$\frac{4}{k}$),
所以线段ST的垂直平分线方程为
y+$\frac{4}{k}$=-$\frac{1}{k}$(x+$\frac{4}{{k}^{2}}$-2).令y=0得点Q横坐标为xQ=-2-$\frac{4}{{k}^{2}}$,
xQ=-2-$\frac{4}{{k}^{2}}$<-6.,所以Q点横坐标的取值范围为(-∞,-6).
点评 本题主要考查轨迹方程的求法,直线和圆锥曲线相交的性质,韦达定理的应用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
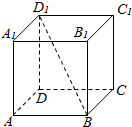 如图,在正方形ABCD-A1B1C1D1中,若平面a平行于该正方体的体对角线BD,则平面a在该正方体上截得的图形不可能为②③④(填序号)
如图,在正方形ABCD-A1B1C1D1中,若平面a平行于该正方体的体对角线BD,则平面a在该正方体上截得的图形不可能为②③④(填序号)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com