
ЁОЬтФПЁПвбжЊЕШБШЪ§Са{an}ЕФЙЋБШЮЊqЃЌМЧbn=amЃЈnЉ1ЃЉ+1+amЃЈnЉ1ЃЉ+2+Ё+amЃЈnЉ1ЃЉ+m ЃЌ cn=amЃЈnЉ1ЃЉ+1amЃЈnЉ1ЃЉ+2ЁamЃЈnЉ1ЃЉ+m ЃЌ ЃЈmЃЌnЁЪN*ЃЉЃЌдђвдЯТНсТлвЛЖЈе§ШЗЕФЪЧЃЈ ЃЉ
A.Ъ§Са{bn}ЮЊЕШВюЪ§СаЃЌЙЋВюЮЊqm
B.Ъ§Са{bn}ЮЊЕШБШЪ§СаЃЌЙЋБШЮЊq2m
C.Ъ§Са{cn}ЮЊЕШБШЪ§СаЃЌЙЋБШЮЊ ![]()
D.Ъ§Са{cn}ЮЊЕШБШЪ§СаЃЌЙЋБШЮЊ ![]()
ЁОД№АИЁПC
ЁОНтЮіЁПНтЃКЂй ![]() ЃЌЕБq=1ЪБЃЌbn=mamЃЈnЉ1ЃЉ ЃЌ bn+1=mamЃЈnЉ1ЃЉ+m=mamЃЈnЉ1ЃЉ=bn ЃЌ ДЫЪБЪЧГЃЪ§СаЃЌбЁЯюAВЛе§ШЗЃЌбЁЯюBе§ШЗЃЛ
ЃЌЕБq=1ЪБЃЌbn=mamЃЈnЉ1ЃЉ ЃЌ bn+1=mamЃЈnЉ1ЃЉ+m=mamЃЈnЉ1ЃЉ=bn ЃЌ ДЫЪБЪЧГЃЪ§СаЃЌбЁЯюAВЛе§ШЗЃЌбЁЯюBе§ШЗЃЛ
ЕБqЁй1ЪБЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌДЫЪБ
ЃЌДЫЪБ ![]() ЃЌбЁЯюBВЛе§ШЗЃЌ
ЃЌбЁЯюBВЛе§ШЗЃЌ
гжbn+1Љbn= ![]() ЃЌВЛЪЧГЃЪ§ЃЌЙЪбЁЯюAВЛе§ШЗЃЌ
ЃЌВЛЪЧГЃЪ§ЃЌЙЪбЁЯюAВЛе§ШЗЃЌ
ЂкЁпЕШБШЪ§Са{an}ЕФЙЋБШЮЊqЃЌЁр ![]() ЃЌ
ЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
Ёр ![]() =
= 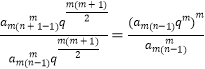 =
= ![]() ЃЌЙЪCе§ШЗDВЛе§ШЗЃЎ
ЃЌЙЪCе§ШЗDВЛе§ШЗЃЎ
злЩЯПЩжЊЃКжЛгаCе§ШЗЃЎ
ЙЪбЁCЃЎ
ЁОПМЕуОЋЮіЁПИљОнЬтФПЕФвбжЊЬѕМўЃЌРћгУЕШВюЙиЯЕЕФШЗЖЈКЭЕШБШЙиЯЕЕФШЗЖЈЕФЯрЙижЊЪЖПЩвдЕУЕНЮЪЬтЕФД№АИЃЌашвЊеЦЮеШчЙћвЛИіЪ§СаДгЕк2ЯюЦ№ЃЌУПвЛЯюгыЫќЕФЧАвЛЯюЕФВюЕШгкЭЌвЛИіГЃЪ§ЃЌМД![]() Ѓ
Ѓ![]() =d ЃЌЃЈnЁн2ЃЌnЁЪN
=d ЃЌЃЈnЁн2ЃЌnЁЪN![]() ЃЉФЧУДетИіЪ§СаОЭНазіЕШВюЪ§СаЃЛЕШБШЪ§СаПЩвдЭЈЙ§ЖЈвхЗЈЁЂжаЯюЗЈЁЂЭЈЯюЙЋЪНЗЈЁЂЧАnЯюКЭЗЈНјааХаЖЯЃЎ
ЃЉФЧУДетИіЪ§СаОЭНазіЕШВюЪ§СаЃЛЕШБШЪ§СаПЩвдЭЈЙ§ЖЈвхЗЈЁЂжаЯюЗЈЁЂЭЈЯюЙЋЪНЗЈЁЂЧАnЯюКЭЗЈНјааХаЖЯЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФађКХЪЧ__________ЃЎ
ЂйгУ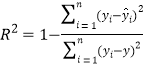 ПЬЛЛиЙщаЇЙћЃЌЕБ
ПЬЛЛиЙщаЇЙћЃЌЕБ ![]() дНДѓЪБЃЌФЃаЭЕФФтКЯаЇЙћдНВюЃЛЗДжЎЃЌдђдНКУЃЛ
дНДѓЪБЃЌФЃаЭЕФФтКЯаЇЙћдНВюЃЛЗДжЎЃЌдђдНКУЃЛ
ЂкПЩЕМКЏЪ§![]() дк
дк![]() ДІШЁМЋжЕЃЌдђ
ДІШЁМЋжЕЃЌдђ![]() ЃЛ
ЃЛ
ЂлЙщФЩЭЦРэЪЧгЩЬиЪтЕНвЛАуЕФЭЦРэЃЌЖјбнвяЭЦРэЪЧгЩвЛАуЕНЬиЪтЕФЭЦРэЃЛ
ЂмзлКЯЗЈжЄУїЪ§бЇЮЪЬтЪЧЁАгЩвђЕМЙћЁБЃЌЗжЮіЗЈжЄУїЪ§бЇЮЪЬтЪЧЁАжДЙћЫївђЁБЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјЖЈЧјгђDЃК  ЃЎСюЕуМЏT={ЃЈx0 ЃЌ y0ЃЉЁЪD|x0 ЃЌ y0ЁЪZЃЌЃЈx0 ЃЌ y0ЃЉЪЧz=x+yдкDЩЯШЁЕУзюДѓжЕЛђзюаЁжЕЕФЕу}ЃЌдђTжаЕФЕуЙВШЗЖЈЬѕВЛЭЌЕФжБЯпЃЎ
ЃЎСюЕуМЏT={ЃЈx0 ЃЌ y0ЃЉЁЪD|x0 ЃЌ y0ЁЪZЃЌЃЈx0 ЃЌ y0ЃЉЪЧz=x+yдкDЩЯШЁЕУзюДѓжЕЛђзюаЁжЕЕФЕу}ЃЌдђTжаЕФЕуЙВШЗЖЈЬѕВЛЭЌЕФжБЯпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕчгАдКЙВга![]() ИізљЮЛ.ФГЬьЃЌетМвЕчгАдКЩЯЁЂЯТЮчИїбнвЛГЁЕчгА.ПДЕчгАЕФЪЧМзЁЂввЁЂБћШ§ЫљжабЇЕФбЇЩњЃЌШ§ЫљбЇаЃЕФЙлгАШЫЪ§ЗжБ№ЪЧ985ШЫЃЌ 1010ШЫЃЌ2019ШЫ(ЭЌвЛЫљбЇаЃЕФбЇЩњгаЕФПДЩЯЮчГЁЃЌвВгаЕФПДЯТЮчГЁЃЌЕЋУПШЫжЛФмПДвЛ-ГЁ).вбжЊЮоТлШчКЮХХзљЮЛЃЌетЬьЙлгАЪБзмДцдкетбљЕФвЛИізљЮЛЃЌЩЯЁЂ ЯТЮчдкетИізљЮЛЩЯзјЕФЪЧЭЌвЛЫљбЇаЃЕФбЇЩњЃЌФЧУД
ИізљЮЛ.ФГЬьЃЌетМвЕчгАдКЩЯЁЂЯТЮчИїбнвЛГЁЕчгА.ПДЕчгАЕФЪЧМзЁЂввЁЂБћШ§ЫљжабЇЕФбЇЩњЃЌШ§ЫљбЇаЃЕФЙлгАШЫЪ§ЗжБ№ЪЧ985ШЫЃЌ 1010ШЫЃЌ2019ШЫ(ЭЌвЛЫљбЇаЃЕФбЇЩњгаЕФПДЩЯЮчГЁЃЌвВгаЕФПДЯТЮчГЁЃЌЕЋУПШЫжЛФмПДвЛ-ГЁ).вбжЊЮоТлШчКЮХХзљЮЛЃЌетЬьЙлгАЪБзмДцдкетбљЕФвЛИізљЮЛЃЌЩЯЁЂ ЯТЮчдкетИізљЮЛЩЯзјЕФЪЧЭЌвЛЫљбЇаЃЕФбЇЩњЃЌФЧУД![]() ЕФПЩФмШЁжЕга( )
ЕФПЩФмШЁжЕга( )
A. 12Иі B. 11Иі C. 10Иі D. ЧАШ§ИіД№АИЖМВЛЖд
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЮЊВтЕУКгЖдАЖЫў![]() ЕФИпЃЌЯШдкКгАЖЩЯбЁвЛЕу
ЕФИпЃЌЯШдкКгАЖЩЯбЁвЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() дкЫўЕз
дкЫўЕз![]() ЕФе§ЖЋЗНЯђЩЯЃЌВтЕУЕу
ЕФе§ЖЋЗНЯђЩЯЃЌВтЕУЕу![]() ЕФбіНЧЮЊ60ЁуЃЌдйгЩЕу
ЕФбіНЧЮЊ60ЁуЃЌдйгЩЕу![]() биББЦЋЖЋ15ЁуЗНЯђзп
биББЦЋЖЋ15ЁуЗНЯђзп![]() ЕНЮЛжУ
ЕНЮЛжУ![]() ЃЌВтЕУ
ЃЌВтЕУ![]() ЃЌдђЫў
ЃЌдђЫў![]() ЕФИпЪЧЃЈЕЅЮЛЃК
ЕФИпЪЧЃЈЕЅЮЛЃК![]() ЃЉЃЈ ЃЉ
ЃЉЃЈ ЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D. 10
D. 10
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
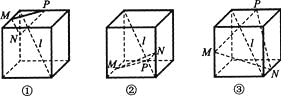
ЁОЬтФПЁПЯТСаЮхИіе§ЗНЬхЭМаЮжаЃЌ![]() ЪЧе§ЗНЬхЕФвЛЬѕЖдНЧЯпЃЌЕуMЃЌNЃЌPЗжБ№ЮЊЦфЫљдкРтЕФжаЕуЃЌЧѓФмЕУГі
ЪЧе§ЗНЬхЕФвЛЬѕЖдНЧЯпЃЌЕуMЃЌNЃЌPЗжБ№ЮЊЦфЫљдкРтЕФжаЕуЃЌЧѓФмЕУГі![]() ЁЭУцMNPЕФЭМаЮЕФађКХ(аДГіЫљгаЗћКЯвЊЧѓЕФЭМаЮађКХ)
ЁЭУцMNPЕФЭМаЮЕФађКХ(аДГіЫљгаЗћКЯвЊЧѓЕФЭМаЮађКХ)

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕу![]() КЭЯђСП
КЭЯђСП![]()
ЃЈ1ЃЉШєЯђСП![]() гыЯђСП
гыЯђСП![]() ЭЌЯђЃЌЧв
ЭЌЯђЃЌЧв![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉШєЯђСП![]() гыЯђСП
гыЯђСП![]() ЕФМаНЧЪЧЖлНЧЃЌЧѓЪЕЪ§
ЕФМаНЧЪЧЖлНЧЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкФГДЮВтЪджаЃЌОэУцТњЗжЮЊ100ЗжЃЌПМЩњЕУЗжЮЊећЪ§ЃЌЙцЖЈ60ЗжМАвдЩЯЮЊМАИё.ФГЕїбаПЮЬтаЁзщЮЊСЫЕїВщЮчанЖдПМЩњИДЯАаЇЙћЕФгАЯьЃЌЖдЮчанКЭВЛЮчанЕФПМЩњНјааСЫВтЪдГЩМЈЕФЭГМЦЃЌЪ§ОнШчЯТБэЃК

ЃЈ1ЃЉИљОнЩЯЪіБэИёЭъГЩЯТСаСаСЊБэЃК
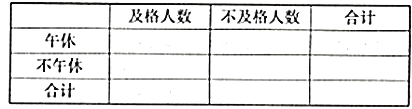
ЃЈ2ЃЉХаЖЯЁАФмЗёдкЗИДэЮѓЕФИХТЪВЛГЌЙ§0.010ЕФЧАЬсЯТШЯЮЊГЩМЈМАИёгыЮчангаЙиЁБЃП
ЃЈВЮПМЙЋЪНЃК![]() ЃЌЦфжа
ЃЌЦфжа![]() .ЃЉ
.ЃЉ
| 0.010 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєІСЪЧЕквЛЯѓЯоНЧЃЌдђsinІС+cosІСЕФжЕгы1ЕФДѓаЁЙиЯЕЪЧЃЈ ЃЉ
A. sinІС+cosІСЃО1B. sinІС+cosІС=1C. sinІС+cosІСЃМ1D. ВЛФмШЗЖЈ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com