
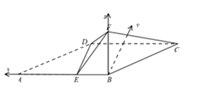
【题目】如图,四边形ABCD为平行四边形,点E在AB上,AE=2EB=2,且DE⊥AB.以DE为折痕把△ADE折起,使点A到达点F的位置,且∠FEB=60°.
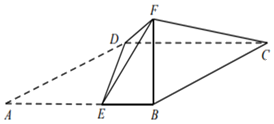
(1)求证:平面BFC⊥平面BCDE;
(2)若直线DF与平面BCDE所成角的正切值为![]() ,求二面角E﹣DF﹣C的正弦值.
,求二面角E﹣DF﹣C的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)首先通过证明![]() 平面
平面![]() 证得
证得![]() .结合余弦定理和勾股定理证得
.结合余弦定理和勾股定理证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,进而证得平面
,进而证得平面![]() 平面
平面![]() .
.
(2)建立空间直角坐标系,由直线![]() 与平面
与平面![]() 所成角的正切值求得正弦值,结合直线
所成角的正切值求得正弦值,结合直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量列方程,解方程求得
的法向量列方程,解方程求得![]() 的长.由此通过平面
的长.由此通过平面![]() 和平面
和平面![]() 的法向量,计算出二面角
的法向量,计算出二面角![]() 的余弦值,进而求得其正弦值.
的余弦值,进而求得其正弦值.
(1)证明:∵DE⊥AB,∴DE⊥EB,DE⊥EF,
∴DE⊥平面BEF,∴DE⊥BF,
∵AE=2EB=2,∴EF=2,EB=1,
∵∠FEB=60°,∴由余弦定理得BF![]() ,
,
∴EF2=EB2+BF2,∴FB⊥EB,
由①②得BF⊥平面BCDE,
∴平面BFC⊥平面BCDE.
(2)解:以B为原点,BA为x轴,在平面ABCD中过点B作AB的垂线为y轴,BF为z轴,建立空间直角坐标系,
设DE=a,则D(1,a,0),F(0,0,![]() ),
),![]() (﹣1,﹣a,
(﹣1,﹣a,![]() ),
),
∵直线DF与平面BCDE所成角的正切值为![]() ,
,
∴直线DF与平面BCDE所成角的正弦值为![]() ,
,
平面BCDE的法向量![]() (0,0,1),
(0,0,1),
∴|cos![]() |
|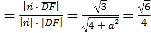 ,解得a=2,
,解得a=2,
∴D(1,2,0),C(﹣2,2,0),∴![]() (0,2,0),
(0,2,0),![]() (﹣1,﹣2,
(﹣1,﹣2,![]() ),
),
设平面EDF的法向量![]() (x,y,z),
(x,y,z),
则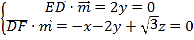 ,取z=1,得
,取z=1,得![]() (
(![]() ),
),
同理得平面DFC的一个法向量![]() (0,
(0,![]() ,2),
,2),
∴cos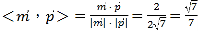 ,
,
∴二面角E﹣DF﹣C的正弦值为sin![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】为了解运动健身减肥的效果,某健身房调查了20名肥胖者,健身之前他们的体重情况如三维饼图(1)所示,经过四个月的健身后,他们的体重情况如三维饼图(2)所示.对比健身前后,关于这20名肥胖者,下面结论不正确的是( )
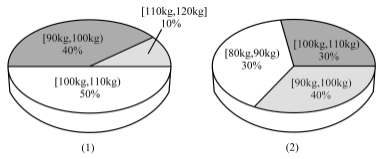
A.他们健身后,体重在区间[90kg,100kg)内的人数不变
B.他们健身后,体重在区间[100kg,110kg)内的人数减少了4人
C.他们健身后,这20位健身者体重的中位数位于[90kg,100kg)
D.他们健身后,原来体重在[110kg,120kg]内的肥胖者体重都至少减轻了10kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研发投入.为了对新研发的产品进行合理定价,将该产品按事先拟定的价格试销,得到一组检测数据如表所示:
试销价格 |
|
|
|
|
|
|
产品销量 |
|
|
|
|
|
|
已知变量![]() 且有线性负相关关系,现有甲、乙、丙三位同学通过计算求得回归直线方程分别为:甲
且有线性负相关关系,现有甲、乙、丙三位同学通过计算求得回归直线方程分别为:甲![]() ; 乙
; 乙![]() ;丙
;丙![]() ,其中有且仅有一位同学的计算结果是正确的.
,其中有且仅有一位同学的计算结果是正确的.
(1)试判断谁的计算结果正确?
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过![]() ,则称该检测数据是“理想数据”,现从检测数据中随机抽取
,则称该检测数据是“理想数据”,现从检测数据中随机抽取![]() 个,求“理想数据”的个数为
个,求“理想数据”的个数为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据历年大学生就业统计资料显示:某大学理工学院学生的就业去向涉及公务员、教师、金融、商贸、公司和自主创业等六大行业.2020届该学院有数学与应用数学、计算机科学与技术和金融工程等三个本科专业,毕业生人数分别是70人,140人和210人.现采用分层抽样的方法,从该学院毕业生中抽取18人调查学生的就业意向.
(1)应从该学院三个专业的毕业生中分别抽取多少人?
(2)国家鼓励大学生自主创业,在抽取的18人中,含有“自主创业”就业意向的有6人,且就业意向至少有三个行业的学生有7人.为方便统计,将至少有三个行业就业意向的这7名学生分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,统计如下表:
,统计如下表:
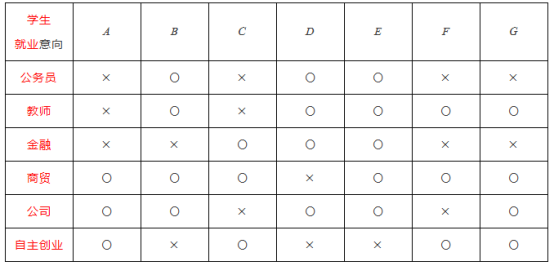
其中“○”表示有该行业就业意向,“×”表示无该行业就业意向.
①试估计该学院2020届毕业生中有自主创业意向的学生人数;
②现从![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这7人中随机抽取2人接受采访.设
这7人中随机抽取2人接受采访.设![]() 为事件“抽取的2人中至少有一人有自主创业意向”,求事件
为事件“抽取的2人中至少有一人有自主创业意向”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某湿地公园内有一条河,现打算建一座桥将河两岸的路连接起来,剖面设计图纸如下:

其中,点![]() 为
为![]() 轴上关于原点对称的两点,曲线段
轴上关于原点对称的两点,曲线段![]() 是桥的主体,
是桥的主体,![]() 为桥顶,且曲线段
为桥顶,且曲线段![]() 在图纸上的图形对应函数的解析式为
在图纸上的图形对应函数的解析式为![]() ,曲线段
,曲线段![]() 均为开口向上的抛物线段,且
均为开口向上的抛物线段,且![]() 分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(
分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(![]() )的切线的斜率相等.
)的切线的斜率相等.
(1)求曲线段![]() 在图纸上对应函数的解析式,并写出定义域;
在图纸上对应函数的解析式,并写出定义域;
(2)车辆从![]() 经
经![]() 倒
倒![]() 爬坡,定义车辆上桥过程中某点
爬坡,定义车辆上桥过程中某点![]() 所需要的爬坡能力为:
所需要的爬坡能力为:![]() (该点
(该点![]() 与桥顶间的水平距离)
与桥顶间的水平距离)![]() (设计图纸上该点处的切线的斜率),其中
(设计图纸上该点处的切线的斜率),其中![]() 的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为
的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为![]() 米,
米,![]() 米,
米,![]() 米,又已知图纸上一个单位长度表示实际长度
米,又已知图纸上一个单位长度表示实际长度![]() 米,试问三种类型的观光车是否都可以顺利过桥?
米,试问三种类型的观光车是否都可以顺利过桥?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,前n项和为
,前n项和为![]() ,且
,且![]() .
.
(1)求![]() ;
;
(2)证明数列![]() 为等差数列,并写出其通项公式;
为等差数列,并写出其通项公式;
(3)设![]() ,试问是否存在正整数p,q(其中
,试问是否存在正整数p,q(其中![]() ),使
),使![]()
![]()
![]() 成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记无穷数列![]() 的前
的前![]() 项中最大值为
项中最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]() ,则称
,则称![]() 是
是![]() “极差数列”.
“极差数列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 项和;
项和;
(2)证明:![]() 的“极差数列”仍是
的“极差数列”仍是![]() ;
;
(3)求证:若数列![]() 是等差数列,则数列
是等差数列,则数列![]() 也是等差数列.
也是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某搜索引擎广告按照付费价格对搜索结果进行排名,点击一次付费价格排名越靠前,被点击的次数也可能会提高,已知某关键词被甲、乙等多个公司竞争,其中甲、乙付费情况与每小时点击量结果绘制成如下的折线图.
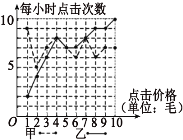
(1)若甲公司计划从这10次竞价中随机抽取3次竞价进行调研,其中每小时点击次数超过7次的竞价抽取次数记为![]() ,求
,求![]() 的分布列与数学期望;
的分布列与数学期望;
(2)若把乙公司设置的每次点击价格为x,每小时点击次数为![]() ,则点
,则点![]() 近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线
近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线![]() .(附:回归方程系数公式:
.(附:回归方程系数公式: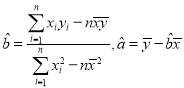
![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com