
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到数据如表所示(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | 8 | |
不肥胖 | 18 | ||
合计 | 30 |
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
| 0.050 0.010 |
| 3.841 6.635 |
参考数据:
附:![]()
科目:高中数学 来源: 题型:
【题目】已知四棱锥P - ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC![]()
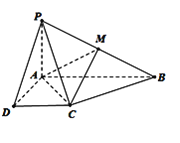
(1)证明平面PAD⊥平面PCD;
(2)求AC与PB所成角的余弦值;
(3)求平面AMC与平面BMC所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1. 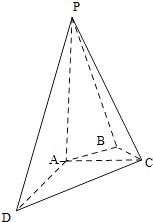
(1)证明:PC⊥AD;
(2)求二面角A﹣PC﹣D的正弦值;
(3)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设四棱锥P-ABCD的底面不是平行四边形,用平面![]() 去截此四棱锥,使得截面是平行四边形,则这样的平面
去截此四棱锥,使得截面是平行四边形,则这样的平面![]() ( )
( )
A.不存在
B.有且只有1个
C.恰好有4个
D.有无数多个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=logm![]() (m>0且m≠1),
(m>0且m≠1),
(I)判断f(x)的奇偶性并证明;
(II)若m=![]() ,判断f(x)在(3,+∞)的单调性(不用证明);
,判断f(x)在(3,+∞)的单调性(不用证明);
(III)若0<m<1,是否存在β>α>0,使f(x)在[α,β]的值域为[logmm(β-1),logm(α-1)]?若存在,求出此时m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m,n是两条不同直线,![]() ,
,![]() 是两个不同平面,则下列命题正确的是
是两个不同平面,则下列命题正确的是
A.若![]() ,
,![]() 垂直于同一平面,则
垂直于同一平面,则![]() 与
与![]() 平行
平行
B.若m,n平行于同一平面,则m与n平行
C.若![]() ,
,![]() 不平行,则在
不平行,则在![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
D.若m,n不平行,则m与n不可能垂直于同一平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
平面直角坐标系xOy中,曲线C:![]() .直线l经过点P(m,0),且倾斜角为
.直线l经过点P(m,0),且倾斜角为![]() .O为极点,以x轴正半轴为极轴,建立极坐标系.
.O为极点,以x轴正半轴为极轴,建立极坐标系.
(Ⅰ)写出曲线C的极坐标方程与直线l的参数方程;
(Ⅱ)若直线l与曲线C相交于A,B两点,且|PA|·|PB|=1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面图形ABB1A1C1C如图4所示,其中BB1C1C是矩形,BC=2,BB1=4,AB=AC= ![]() ,A1B1=A1C1=
,A1B1=A1C1= ![]() .现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
.现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
(Ⅰ)证明:AA1⊥BC;
(Ⅱ)求AA1的长;
(Ⅲ)求二面角A﹣BC﹣A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子内装有8张卡片,每张卡片上面写着1个数字,这8个数字各不相同,且奇数有3个,偶数有5个.每张卡片被取出的概率相等.
(Ⅰ)如果从盒子中一次随机取出2张卡片,并且将取出的2张卡片上的数字相加得到一个新数,求所得新数是偶数的概率;
(Ⅱ)现从盒子中一次随机取出1张卡片,每次取出的卡片都不放回盒子,若取出的卡片上写着的数是偶数则停止取出卡片,否则继续取出卡片.设取出了![]() 次才停止取出卡片,求
次才停止取出卡片,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com