
【题目】(1)求经过直线3x+4y-2=0与直线x-y+4=0的交点P,且垂直于直线x-2y-1=0的直线方程;
(2)求过点P(-1,3),并且在两坐标轴上的截距相等的直线方程.
【答案】(1)2x+y+2=0;(2)3x+y=0或x+y-2=0.
【解析】
(1)联立直线方程求出点的坐标,再求出所求直线的斜率,代入直线方程点斜式得答案;
(2)当直线过原点时,直线方程为y=-3x;当直线不过原点时,设直线方程为x+y=a,把点的坐标代入求得a,则直线方程可求.
解:(1)联立![]() ,解得
,解得![]() ,
,
∴两直线的焦点坐标为(-2,2),
直线x-2y-1=0斜率为![]() ,则所求直线的斜率为-2.
,则所求直线的斜率为-2.
∴直线方程为y-2=-2(x+2),
即2x+y+2=0;
(2)当直线过原点时,直线方程为y=-3x;
当直线不过原点时,设直线方程为x+y=a,则-1+3=a,即a=2.
是求直线方程为x+y=2.
∴所求直线方程为3x+y=0或x+y-2=0.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】为创建全国文明城市,我市积极打造“绿城”的创建目标,使城市环境绿韵萦绕,使市民生活绿意盎然.有效增加城区绿化面积,提高城区绿化覆盖率,提升城市形象品位.林业部门推广种植甲、乙两种树苗,并对甲、乙两种树苗各抽测了10株树苗的高度(单位:厘米),数据如下面的茎叶图:

(1)根据茎叶图求甲、乙两种树苗的平均高度;
(2)根据茎叶图,计算甲、乙两种树苗的高度的方差,运用统计学知识分析比较甲、乙两种树苗高度整齐情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
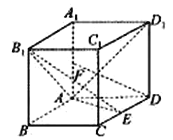
【题目】如图,四棱柱![]() 的底面为菱形,
的底面为菱形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 底面
底面![]() ,且直线
,且直线![]() 与平面
与平面![]() 所成线面角的正弦值为
所成线面角的正弦值为![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)2.
【解析】试题分析:(1)设![]() 为
为![]() 的中点,根据平几知识可得四边形
的中点,根据平几知识可得四边形![]() 是平行四边形,即得
是平行四边形,即得![]() ,再根据线面平行判定定理得结论,(2)根据条件建立空间直角坐标系,设立各点坐标,利用方程组解得平面
,再根据线面平行判定定理得结论,(2)根据条件建立空间直角坐标系,设立各点坐标,利用方程组解得平面![]() 一个法向量,根据向量数量积求向量夹角,再根据线面角与向量夹角互余关系列等式,解得
一个法向量,根据向量数量积求向量夹角,再根据线面角与向量夹角互余关系列等式,解得![]() 的长.
的长.
试题解析:(1)证明:设![]() 为
为![]() 的中点,连
的中点,连![]()
因为![]()
![]()
![]() ,又
,又![]()
![]()
![]() ,所以
,所以![]()
![]()
![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
所以![]()
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
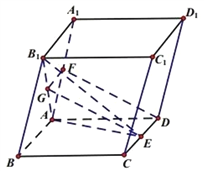
(2)因为![]() 是菱形,且
是菱形,且![]() ,
,
所以![]() 是等边三角形
是等边三角形
取![]() 中点
中点![]() ,则
,则![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() ,
, ![]()
建立如图的空间直角坐标系,令![]() ,
,
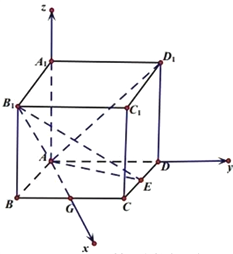
则![]() ,
, 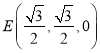 ,
, ![]() ,
, ![]() ,
,
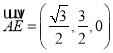 ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() 且
且![]() ,
,
取![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则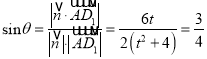 ,
,
解得![]() ,故线段
,故线段![]() 的长为2.
的长为2.
【题型】解答题
【结束】
20
【题目】椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,若椭圆过点
,若椭圆过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
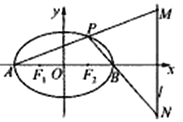
(2)若![]() 为椭圆的左、右顶点,
为椭圆的左、右顶点, ![]() (
(![]() )为椭圆上一动点,设直线
)为椭圆上一动点,设直线![]() 分别交直线
分别交直线![]() :
: ![]() 于点
于点![]() ,判断线段
,判断线段![]() 为直径的圆是否经过定点,若是,求出该定点坐标;若不恒过定点,说明理由.
为直径的圆是否经过定点,若是,求出该定点坐标;若不恒过定点,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点为
的一个焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程与离心率;
的方程与离心率;
(Ⅱ)设椭圆![]() 上不与
上不与![]() 点重合的两点
点重合的两点![]() ,
, ![]() 关于原点
关于原点![]() 对称,直线
对称,直线![]() ,
, ![]() 分别交
分别交![]() 轴于
轴于![]() ,
, ![]() 两点.求证:以
两点.求证:以![]() 为直径的圆被
为直径的圆被![]() 轴截得的弦长是定值.
轴截得的弦长是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ∥
∥![]() ,
, ![]() 为
为![]() 中点.
中点.
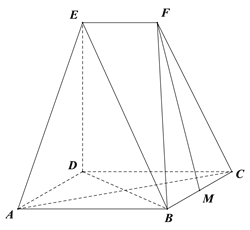
(1)求证: ![]() ∥平面
∥平面![]() ;
;
(2)求证: ![]() ;
;
(3)若![]() 为线段
为线段![]() 上的点,当三棱锥
上的点,当三棱锥![]() 的体积为
的体积为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,在梯形
,在梯形![]() 中,
中, ![]() 于
于![]() ,
, ![]()
![]() .将
.将![]() 沿
沿![]() 折起至
折起至![]() ,使得平面
,使得平面![]() 平面
平面![]() (如图2),
(如图2), ![]() 为线段
为线段![]() 上一点.
上一点.
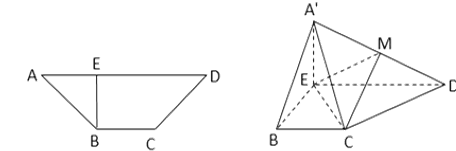
图1 图2
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() 为线段
为线段![]() 中点,求多面体
中点,求多面体![]() 与多面体
与多面体![]() 的体积之比;
的体积之比;
(Ⅲ)是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的长.若不存在,请说明理由.
的长.若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
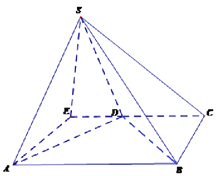
【题目】四棱锥![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为正三角形.
为正三角形.
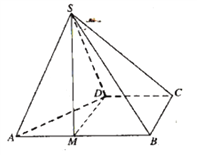
(1)点![]() 为棱
为棱![]() 上一点,若
上一点,若![]() 平面
平面![]() ,
,![]() ,求实数
,求实数![]() 的值;
的值;
(2)求点B到平面SAD的距离.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由![]() 平面
平面![]() ,可证
,可证![]() ,进而证得四边形
,进而证得四边形![]() 为平行四边形,根据
为平行四边形,根据![]() ,可得
,可得![]() ;
;
(2)利用等体积法![]() 可求点
可求点![]() 到平面
到平面![]() 的距离.
的距离.
试题解析:((1)因为![]() 平面SDM,
平面SDM,
![]()
![]() 平面ABCD,
平面ABCD,
平面SDM ![]() 平面ABCD=DM,
平面ABCD=DM,
所以![]() ,
,
因为![]() ,所以四边形BCDM为平行四边形,又
,所以四边形BCDM为平行四边形,又![]() ,所以M为AB的中点.
,所以M为AB的中点.
因为![]() ,
,
![]() .
.
(2)因为![]()
![]() ,
, ![]()
![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
在平面![]() 内过点
内过点![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() ,
,
在![]() 和
和![]() 中,
中,
因为![]() ,所以
,所以![]() ,
,
又由题知![]() ,
,
所以![]() ,
,
由已知求得![]() ,所以
,所以![]() ,
,
连接BD,则![]() ,
,
又求得![]() 的面积为
的面积为![]() ,
,
所以由![]() 点B 到平面
点B 到平面![]() 的距离为
的距离为![]() .
.
【题型】解答题
【结束】
19
【题目】小明在石家庄市某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元.
(1)请分别求出甲、乙两种薪酬方案中日薪![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
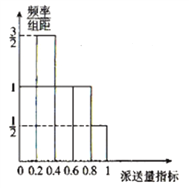
(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在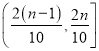
![]() 时,日平均派送量为
时,日平均派送量为![]() 单.
单.
若将频率视为概率,回答下列问题:
①根据以上数据,设每名派送员的日薪为![]() (单位:元),试分别求出甲、乙两种方案的日薪
(单位:元),试分别求出甲、乙两种方案的日薪![]() 的分布列,数学期望及方差;
的分布列,数学期望及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由.
(参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上任一点,
上任一点, ![]() 为其右焦点,
为其右焦点, ![]() 是椭圆的左、右顶点,点
是椭圆的左、右顶点,点![]() 满足
满足![]() .
.
①证明: ![]() 为定值;
为定值;
②设![]() 是直线
是直线![]() 上的任一点,直线
上的任一点,直线![]() 分别另交椭圆
分别另交椭圆![]() 于
于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com