练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用样本频率分布直方图估计总体密度曲线，可分为两种情况：

    第一类：“总体中的个体取不同数值很少”，几何表示为________，条形图的________表示取各个值的频率；

    第二类：“总体中的个体取不同值较多，甚至无限”，几何表示为________，频率分布为各不同区间内取值的频率，相应长方形面积的大小来表示在各个区间内取值的频率．

    总体中个体落入区间(a，b)的概率等于区间(a，b)对应的总体密度曲线下方的________．

    答案：相应的条形图,高度,无间隔直方图,面积
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩，按成绩共分成五组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，得到的频率分布直方图如图所示，同时规定成绩在85分以上（含85分）的学生为“优秀”，成绩小于85分的学生为“良好”，且只有成绩为“优秀”的学生才能获得面试资格．
    （1）求出第4组的频率，并补全频率分布直方图；
    （2）根据样本频率分布直方图估计样本的中位数；
    （3）如果用分层抽样的方法从“优秀”和“良好”的学生中选出5人，再从这5人中选2人，那么至少有一人是“优秀”的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

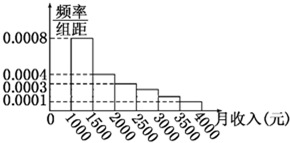    如图是某市有关部门根据该市干部的月收入情况，作抽样调查后画出的样本频率分布直方图，已知图中第一组的频数为4 000，请根据该图提供的信息解答下列问题：图中每组包括左端点，不包括右端点，如第一组表示收入在[1 000，1 500）．
    （1）求样本中月收入在[2 500，3 500）的人数．
    （2）为了分析干部的收入与年龄、职业等方面的关系，必须从样本的各组中按月收入再用分层抽样方法抽出100人作进一步分析，则月收入在[1 500，2 000）的这段应抽多少人？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

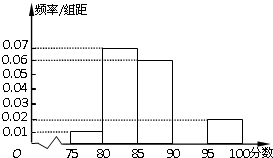    精英家教网校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩，按成绩共分成五组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，得到的频率分布直方图如图所示，同时规定成绩在85分以上的学生为“优秀”，成绩小于85分的学生为“良好”，且只有成绩为“优秀”的学生才能获得面试资格．
    （Ⅰ）求出第4组的频率，并补全频率分布直方图；
    （Ⅱ）根据样本频率分布直方图估计样本的中位数与平均数；
    （Ⅲ）如果用分层抽样的方法从“优秀”和“良好”的学生中共选出5人，再从这5人中选2人，那么至少有一人是“优秀”的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：022

    用样本频率分布直方图估计总体密度曲线，可分为两种情况：

    第一类：“总体中的个体取不同数值很少”，几何表示为________，条形图的________表示取各个值的频率；

    第二类：“总体中的个体取不同值较多，甚至无限”，几何表示为________，频率分布为各不同区间内取值的频率，相应长方形面积的大小来表示在各个区间内取值的频率．

    总体中个体落入区间(a，b)的概率等于区间(a，b)对应的总体密度曲线下方的________．

    查看答案和解析>>

    同步练习册答案