【题目】为了推进课堂改革，提高课堂效率，银川一中引进了平板教学，开始推进“智慧课堂”改革.学校教务处为了了解我校高二年级同学平板使用情况，从高二年级923名同学中抽取50名同学进行调查．先用简单随机抽样从923人中剔除23人，剩下的900人再按系统抽样方法抽取50人，则在这923人中，每个人被抽取的可能性 ( )
A.都相等，且为
B.不全相等C.都相等，且为
D.都不相等
ABC考王全优卷系列答案科目：高中数学 来源： 题型：
【题目】给定平面上的点集
，
中任三点均不共线。将中所有的点任意分成83组，使得每组至少有3个点，且每点恰好属于一组，然后将在同一组的任两点用一条线段相连，不在同一组的两点不连线段，这样得到一个图案
。不同的分组方式得到不同的图案。将图案中所含的以中的点为顶点的三角形的个数记为
。
（1）求的最小值
；
（2）设
是使
的一个图案，若将中的线段（指以的点为端点的线段）用4种颜色染色，每条线段恰好染一种颜色。证明存在一个染色方案，使染色后不含以的点为顶点的三边颜色相同的三角形。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，三棱柱
的各棱长均为2，侧面
底面
，侧棱
与底面所成的角为
．
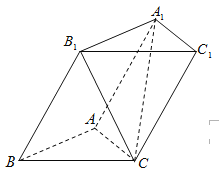
（Ⅰ）求直线
与底面所成的角；
（Ⅱ）在线段
上是否存在点
，使得平面
平面
？若存在，求出
的长；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系中，圆
：
经过伸缩变换
，后得到曲线
以坐标原点为极点，x轴的正半轴为极轴，并在两种坐标系中取相同的单位长度，建立极坐标系，直线l的极坐标方程为
求曲线的直角坐标方程及直线l的直角坐标方程；
在上求一点M，使点M到直线l的距离最小，并求出最小距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“双十一”期间，某淘宝店主对其商品的上架时间
（小时）和销售量
（件）的关系作了统计，得到了如下数据并研究.
上架时间 | 2 | 4 | 6 | 8 | 10 | 12 |
销售量 | 64 | 138 | 205 | 285 | 360 | 430 |
（1）求表中销售量
的平均数和中位数；
（2）① 作出散点图，并判断变量
与
是否线性相关？若研究的方案是先根据前5组数据求线性回归方程，再利用第6组数据进行检验，求线性回归方程
；
②若根据①中线性回归方程得到商品上架12小时的销售量的预测值与检测值不超过3件，则认为得到的线性回归方程是理想的，试问：①中的线性回归方程是否理想.
附：线性回归方程
中，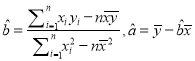 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了保护环境,某工厂在政府部门的支持下,进行技术改进：把二氧化碳转化为某种化工产品,经测算,该处理成本y（万元）与处理量x（吨）之间的函数关系可近似地表示为：
,且每处理一吨二氧化碳可得价值为20万元的某种化工产品．
（1）当
时,判断该技术改进能否获利？如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损？
（2）当处理量为多少吨时,每吨的平均处理成本最少．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（Ⅰ）计算：
①若
是椭圆
长轴的两个端点，
，则
______；
②若是椭圆长轴的两个端点，
，则______；
③若是椭圆长轴的两个端点，
，则______．
（Ⅱ）观察①②③，由此可得到：若是椭圆
长轴的两个端点，
为椭圆上任意一点，则？并证明你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
