
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处与直线
处与直线![]() 相切,求
相切,求![]() 与
与![]() 的值;
的值;
(2)若曲线![]() 与直线
与直线![]() 有两个不同交点,求
有两个不同交点,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过椭圆
,过椭圆![]() 右顶点和上顶点的直线
右顶点和上顶点的直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的上顶点,过点
的上顶点,过点![]() 分别作直线
分别作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为![]() ,且
,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,设倾斜角为
中,设倾斜角为![]() 的直线
的直线![]() 为参数)与曲线
为参数)与曲线![]() 为参数)相交于不同的两点
为参数)相交于不同的两点![]() .
.
(1)若![]() ,求线段
,求线段![]() 中点
中点![]() 的坐标;
的坐标;
(2)若![]() ,其中
,其中![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴, 建立平面直角坐标系,在平面直角坐标系
轴的正半轴, 建立平面直角坐标系,在平面直角坐标系![]() 中, 直线
中, 直线![]() 经过点
经过点![]() ,倾斜角
,倾斜角![]() .
.
(1)写出曲线![]() 直角坐标方程和直线
直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点, 求
两点, 求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三上学期期末数学考试成绩中,随机抽取了![]() 名学生的成绩得到频率分布直方图如下:
名学生的成绩得到频率分布直方图如下:
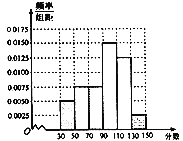
(1)若用分层抽样的方法从分数在![]() 和
和![]() 的学生中共抽取
的学生中共抽取![]() 人,该
人,该![]() 人中成绩在
人中成绩在![]() 的有几人?
的有几人?
(2)在(1)中抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求分数在
人,求分数在![]() 和
和![]() 各
各![]() 人的概率.
人的概率.
(3)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
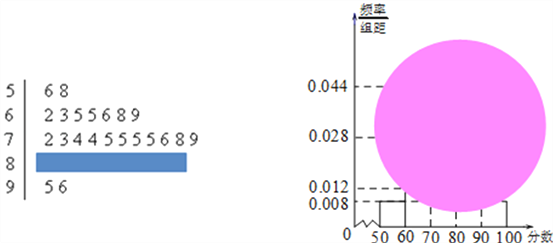
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程
:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,
,![]() 和
和![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:

他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是
A. 289 B. 1 024 C. 1 225 D. 1 378
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com