
【题目】已知圆C的方程:x2+y2﹣2x﹣4y+m=0,其中m<5.
(1)若圆C与直线l:x+2y﹣4=0相交于M,N两点,且|MN|= ![]() ,求m的值;
,求m的值;
(2)在(1)条件下,是否存在直线l:x﹣2y+c=0,使得圆上有四点到直线l的距离为 ![]() ,若存在,求出c的范围,若不存在,说明理由.
,若存在,求出c的范围,若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.若p∨q为真命题,则p∧q为真命题
B.“x=5”是“x2﹣4x﹣5=0”的充分不必要条件
C.命题“若x<﹣1,则x2﹣2x﹣3>0”的否定为:“若x≥﹣1,则x2﹣2x﹣3≤0”
D.已知命题 p:x∈R,x2+x﹣1<0,则p:x∈R,x2+x﹣1≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn=a2n+b,且a1=3.
(1)求a、b的值及数列{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=loga(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中m,n均大于0,则 ![]() 的最小值为( )
的最小值为( )
A.2
B.4
C.8
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》有如下问题:有上禾三秉(古代容量单位),中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗.问上、中、下禾一秉各几何?依上文:设上、中、下禾一秉分别为x斗、y斗、z斗,设计如图所示的程序框图,则输出的x,y,z的值分别为( ) 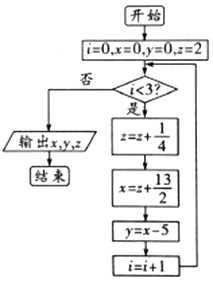
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com