
【题目】设二次函数f(x)=ax2+bx+c(a≠0)在区间[﹣2,2]上的最大值、最小值分别是M,m,集合A={x|f(x)=x}.
(1)若A={1,2},且f(0)=2,求M和m的值;
(2)若A={1},且a≥1,记g(a)=M+m,求g(a)的最小值.
【答案】
(1)解:由f(0)=2可知c=2,
又A={1,2},故1,2是方程ax2+(b﹣1)x+c=0的两实根.
∴ 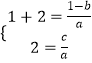 ,解得a=1,b=﹣2
,解得a=1,b=﹣2
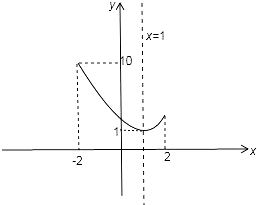
∴f(x)=x2﹣2x+2=(x﹣1)2+1,
因为x∈[﹣2,2],根据函数图象可知,当x=1时,
f(x)min=f(1)=1,即m=1;
当x=﹣2时,f(x)max=f(﹣2)=10,即M=10
(2)解:由题意知,方程ax2+(b﹣1)x+c=0有两相等实根x1=x2=1,
根据韦达定理得到: 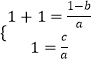 ,即
,即 ![]() ,
,
∴f(x)=ax2+bx+c=ax2+(1﹣2a)x+a,x∈[﹣2,2]其对称轴方程为x= ![]() =1﹣
=1﹣ ![]()
又a≥1,故1﹣ ![]()
∴M=f(﹣2)=9a﹣2
m= ![]()
则g(a)=M+m=9a﹣ ![]() ﹣1
﹣1
又g(a)在区间[1,+∞)上为单调递增的,∴当a=1时,g(a)min= ![]()
【解析】(1)由f(0)=2得到c的值,集合A的方程可变为f(x)﹣x=0,因为A={1,2},得到1,2是方程的解,根据韦达定理即可求出a和b,把a、b、c代入得到f(x)的解析式,在[﹣2,2]上根据函数的图象可知m和M的值.(2)由集合A={1},得到方程f(x)﹣x=0有两个相等的解都为1,根据韦达定理求出a,b,c的关系式,根据a大于等于1,利用二次函数求最值的方法求出在[﹣2,2]上的m和M,代入g(a)=m+M中得到新的解析式g(a)=9a﹣ ![]() ﹣1,根据g(a)的在[1,+∞)上单调增,求出g(a)的最小值为g(1),求出值即可.
﹣1,根据g(a)的在[1,+∞)上单调增,求出g(a)的最小值为g(1),求出值即可.
【考点精析】关于本题考查的二次函数的图象和二次函数的性质,需要了解二次函数![]() 的图象是一条抛物线,对称轴方程为
的图象是一条抛物线,对称轴方程为![]() 顶点坐标是
顶点坐标是![]() ;当
;当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能得出正确答案.
上递减才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某商品在近30天内每件的销售价格P(元)与时间t(天)的函数是:P= ![]()
该商品的日销售量Q(件)与时间t(天)的函数关系是:Q=﹣t+40(0<t≤30,t∈N*),求这种商品的日销售金额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z1=(1+bi)(2+i),z2=3+(1﹣a)i(a,b∈R,i为虚数单位).
(1)若z1=z2 , 求实数a,b的值;
(2)若b=1,a=0,求| ![]() |.
|.
查看答案和解析>>
科目:高中数学 来源: 题型:
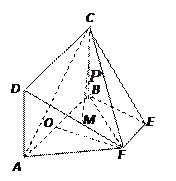
【题目】如图,矩形ABCD所在的平面和平面![]() 互相垂直,等腰梯形
互相垂直,等腰梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点,
的中点, ![]() 为底面
为底面![]() 的重心.
的重心.
(Ⅰ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(x∈R),(a,b为实数).
(1)若f(1)=0,且函数f(x)的值域为[0,+∞),求f(x)的表达式;
(2)在(1)的条件下,若关于x方程|f(x+1)﹣1|=m|x﹣1|只有一个实数解,求实数m的取值范围;
(3)在(1)的条件下,求函数h(x)=2f(x+1)+x|x﹣m|+2m最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
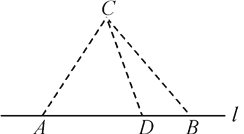
【题目】如图,在海岸线![]() 一侧
一侧![]() 处有一个美丽的小岛,某旅游公司为方便游客,在
处有一个美丽的小岛,某旅游公司为方便游客,在![]() 上设立了
上设立了![]() 两个报名点,满足
两个报名点,满足![]() 中任意两点间的距离为
中任意两点间的距离为![]() .公司拟按以下思路运作:先将
.公司拟按以下思路运作:先将![]() 两处游客分别乘车集中到
两处游客分别乘车集中到![]() 之间的中转点
之间的中转点![]() 处(点
处(点![]() 异于
异于![]() 两点),然后乘同一艘轮游轮前往
两点),然后乘同一艘轮游轮前往![]() 岛.据统计,每批游客
岛.据统计,每批游客![]() 处需发车2辆,
处需发车2辆, ![]() 处需发车4辆,每辆汽车每千米耗费
处需发车4辆,每辆汽车每千米耗费![]() 元,游轮每千米耗费
元,游轮每千米耗费![]() 元.(其中
元.(其中![]() 是正常数)设∠
是正常数)设∠![]() ,每批游客从各自报名点到
,每批游客从各自报名点到![]() 岛所需运输成本为
岛所需运输成本为![]() 元.
元.
(1) 写出![]() 关于
关于![]() 的函数表达式,并指出
的函数表达式,并指出![]() 的取值范围;
的取值范围;
(2) 问:中转点![]() 距离
距离![]() 处多远时,
处多远时, ![]() 最小?
最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com