
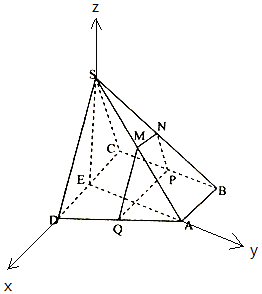
����Ŀ����ͼ������S��ABCD�У�����ABCDΪֱ�����Σ�AB��CD��BC��CD��ƽ��SCD��ƽ��ABCD��SC=SD=CD=AD=2AB��M��N�ֱ�ΪSA��SB���е㣬EΪCD�е㣬��M��N��ƽ��MNPQ�ֱ���BC��AD���ڵ�P��Q���� ![]() =t
=t ![]() ��
�� 
��1����t= ![]() ʱ����֤��ƽ��SAE��ƽ��MNPQ��
ʱ����֤��ƽ��SAE��ƽ��MNPQ��
��2���Ƿ����ʵ��t��ʹ�ö����M��PQ��A��ƽ��ǵ�����ֵΪ ![]() �������ڣ����ʵ��t��ֵ���������ڣ�˵�����ɣ�
�������ڣ����ʵ��t��ֵ���������ڣ�˵�����ɣ�
���𰸡�
��1��֤������1��EΪCD�е㣬���ı���ABCEΪ���Σ�
��AE��CD��
��t= ![]() ʱ��QΪAD�е㣬PQ��CD������PQ��AE��
ʱ��QΪAD�е㣬PQ��CD������PQ��AE��
��ƽ��SCD��ƽ��ABCD��SE��CD����SE����ABCD��
��PQ��ABCD����PQ��SE����PQ����SAE��
������MNPQ����SAE
��2���⣺��ͼ����EΪԭ�㣬ED��EA��ESֱ�߷ֱ�Ϊx�ᣬy�ᣬz�Ὠ����ͼ��ʾ����ϵ��
��ED=a����M����1��t��a���� ![]() ��
�� ![]() ��a��
��a�� ![]() a����E��0��0��0����A��0��
a����E��0��0��0����A��0�� ![]() ��0����
��0����
Q����1��t��a�� ![]() ��0����
��0���� ![]() =��0��
=��0�� ![]() ��
�� ![]() ����
����
��ABCDһ����������Ϊ ![]() =��1��0��0����
=��1��0��0����
��ƽ��MPQ�ķ����� ![]() =��x��y��z����
=��x��y��z����
��  ��ȡz=2����
��ȡz=2���� ![]() =��0��
=��0�� ![]() ��2����
��2����
ƽ��ABCD�ķ�����Ϊ ![]() =��0��0��1��
=��0��0��1��
�߶����M��PQ��A��ƽ��ǵ�����ֵΪ ![]() ��
��
�������⣺cos��= ![]() =
= 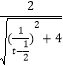 =
= ![]() ��
��
���t= ![]() ��t=
��t= ![]() ��
��
��ͼ��֪����t= ![]() ʱ�������M��PQ��AΪ�۶���ǣ��������⣬��ȥ
ʱ�������M��PQ��AΪ�۶���ǣ��������⣬��ȥ
���ϣ�t= ![]() ��
��
����������1���Ƶ���AE��CD��PQ��AE���Ӷ�SE����ABCD���ɴ���֤����MNPQ����SAE����2����EΪԭ�㣬ED��EA��ESֱ�߷ֱ�Ϊx�ᣬy�ᣬz�Ὠ���ռ�ֱ������ϵ�����������������t��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣����ǰ�һϵ������![]() �������ų�һ�У���֮Ϊ�����У�����
�������ų�һ�У���֮Ϊ�����У�����![]() ����֪������
����֪������![]() ���㣺
���㣺![]() ��
��![]()
![]() ��
��
��1��֤��������![]() �ǵȱ����У�
�ǵȱ����У�
��2����![]() ��ʾ����
��ʾ����![]() ��
��![]() ��ļнǣ���
��ļнǣ���![]() ����������������
����������������![]() ������ʽ
������ʽ ���������ʵ��
���������ʵ��![]() �ķ�Χ
�ķ�Χ
��3����![]() ��������
��������![]() ���Ƿ������С������ڣ������С��������ڣ���˵������
���Ƿ������С������ڣ������С��������ڣ���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=loga��x+3����1��a��0��a��1����ͼ��������A������A��mx+ny+2=0�ϣ�����mn��0���� ![]() ����СֵΪ ��
����СֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x��=. ![]() ��ֱ��x=0��x=e��y=0��y=1��Χ�ɵ�����ΪM������y=f��x����ֱ��y=1Χ�ɵ�����ΪN��������M����ȡһ����P�����P������N�ڸ���Ϊ�� ��
��ֱ��x=0��x=e��y=0��y=1��Χ�ɵ�����ΪM������y=f��x����ֱ��y=1Χ�ɵ�����ΪN��������M����ȡһ����P�����P������N�ڸ���Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������������ij���Ϊ������ɫ���С��ṩ�˼���ķ��㣬ij����������˾��Mobike���ƻ��ڼס����������й�Ͷ��120��Ԫ��������ҵ�涨��ÿ����������ҪͶ��40��Ԫ����ǰ���г����п�֪���׳�������![]() ��Ͷ��
��Ͷ��![]() ����λ����Ԫ������
����λ����Ԫ������![]() ���ҳ�������
���ҳ�������![]() ��Ͷ��
��Ͷ��![]() ����λ����Ԫ������
����λ����Ԫ������![]() ����׳��е�Ͷ��Ϊ
����׳��е�Ͷ��Ϊ![]() ����λ����Ԫ�����������е�������Ϊ
����λ����Ԫ�����������е�������Ϊ![]() ����λ����Ԫ����
����λ����Ԫ����
��1�����׳���Ͷ��50��Ԫʱ�����ʱ��˾�����棻
��2��������ΰ��żס����������е�Ͷ�ʣ�����ʹ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ԭ��OΪ���㣬x���������Ϊ���ᣬ����������ϵ������C1�IJ�������Ϊ ![]() ����Ϊ������������ C2�ļ����귽��Ϊ��cos�ȩ�
����Ϊ������������ C2�ļ����귽��Ϊ��cos�ȩ� ![]() ��sin�ȩ�4=0��
��sin�ȩ�4=0��
��1��������C1����ͨ���̺����� C2��ֱ�����귽�̣�
��2����PΪ����C1��һ�㣬QΪ���� C2��һ�㣬��|PQ|����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ɵ���������![]() ��ʾ��
��ʾ��![]() �е�
�е�![]() ������
������![]() ��. �˱���
��. �˱���![]() ��ÿ���г���β�����⣬���������ֱ�����䡰����ϵ�����֮��.
��ÿ���г���β�����⣬���������ֱ�����䡰����ϵ�����֮��.

��1��д�������ĵ�6��(�������������г�����
��2�����![]() �еĵڶ�����Ϊ
�еĵڶ�����Ϊ![]() ����
����![]() ��
��
��3����![]() ����
����![]() ����
Ϊ����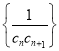 ǰ
ǰ![]() ��ͣ���
��ͣ���![]() �����ֵ�������ʱ
�����ֵ�������ʱ![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����z1 �� z2�Ǹ��������������ĸ����⣺
����|z1��z2|=0���� ![]() =
= ![]() ����z1=
����z1= ![]() ����
���� ![]() =z2
=z2
����|z1|=|z2|����z1 ![]() =z2
=z2 ![]() ����|z1|=|z2|����z12=z22
����|z1|=|z2|����z12=z22
���������������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���Ϊ0�ĵȲ�����{an}��ǰn���ΪSn������S3��a4��4����a2��a6��a18�ɵȱ�������
(1)������{an}��ͨ�ʽ��
(2)��bn��![]() ��������{bn}��ǰn���Tn��
��������{bn}��ǰn���Tn��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com