
分析 求出原函数的导函数,令g(x)=ax2+2(a+1)x+2,问题转化为g(x)≥0在[0,2]恒成立即可,分a=0和a≠0两种情况讨论,
解答 解:由f(x)=(ax2+2x)ex,得
f′(x)=(2ax+2)ex+(ax2+2x)ex=[ax2+2(a+1)x+2]ex,
(1)当a=0时,f′(x)=2(x+1)ex,f′(x)>0在[0,2]上恒成立,
故a=0符合要求;
(2)当a≠0时,令g(x)=ax2+2(a+1)x+2,
因为△=4(a+1)2-4a=4a2+4a+1=(2a+1)2≥0,
①a=-$\frac{1}{2}$时,△=0,g(x)=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2,
f′(x)>0在[0,2]恒成立,
∴a=-$\frac{1}{2}$符合要求;
②a≠-$\frac{1}{2}$时,△>0,
∴g(x)有两个不相等的实数根x1,x2,不妨设x1>x2,
因此f(x)有极大值又有极小值.
若a>0,g(x)的对称轴x=-$\frac{a+1}{a}$<0,g(0)=2>0,
∴g(x)>0在[0,2]恒成立,
若-$\frac{1}{2}$<a<0,对称轴x=-$\frac{a+1}{a}$>1,
g(0)=2,g(2)=8a+6>2>0,
∴g(x)>0在[0,2]恒成立,
∴-$\frac{1}{2}$<a<0符合要求;
a<-$\frac{1}{2}$时,令g(2)=8a+6≥0,解得:a≥-$\frac{3}{4}$,
故-$\frac{3}{4}$≤a<-$\frac{1}{2}$时,g(x)≥0在[0,2]恒成立,
a<-$\frac{3}{4}$时,g(2)<0,g(0)=2>0,
故f(x)在[-1,1]上不单调,
综上,a≥-$\frac{3}{4}$时,f(x)在[0,2]上单调递增.
点评 本题主要考查函数的单调性与其导函数的正负之间的关系,考查了分类讨论的数学思想方法,训练了方程的根与二次函数的图象之间的关系,属中档题.


科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
一个三棱锥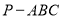 的三条侧棱
的三条侧棱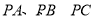 两两互相垂直,且长度分别为1、
两两互相垂直,且长度分别为1、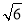 、3,则这个三棱锥的外接球的表面积为( )
、3,则这个三棱锥的外接球的表面积为( )
A.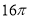 B.
B.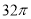 C.
C. 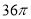 D.
D.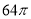
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com