
【题目】已知a,b为常数,且a≠0,f(x)=ax2+bx,f(2)=0,方程f(x)=x有两个相等实数根.
(1)求函数f(x)的解析式;
(2)当x∈[1,2]时,求f(x)的值域;
(3)若F(x)=f(x)-f(-x),试判断F(x)的奇偶性,并证明你的结论.
【答案】(1) f(x)=-![]() x2+x;(2)
x2+x;(2) ![]() ;(3)详见解析.
;(3)详见解析.
【解析】试题分析:(1) 由f(2)=0以及方程f(x)=x有两个相等实数根,求出a,b的值,代入原函数求出解析式;(2)对二次函数f(x)配方, 显然函数f(x)在[1,2]上是减函数,分别求出端点值得出函数的值域;(3)用奇函数的定义判断并证明函数的奇偶性.
试题解析:
(1)已知f(x)=ax2+bx.
由f(2)=0,得4a+2b=0,即2a+b=0①
方程f(x)=x,即ax2+bx=x,
即ax2+(b-1)x=0有两个相等实根,且a≠0,∴b-1=0,∴b=1,代入①得a=-![]() .
.
∴f(x)=-![]() x2+x.
x2+x.
(2)由(1)知f(x)=-![]() (x-1)2+
(x-1)2+![]() .显然函数f(x)在[1,2]上是减函数,
.显然函数f(x)在[1,2]上是减函数,
∴x=1时,ymax=![]() ,x=2时,ymin=0.∴x∈[1,2]时,函数的值域是
,x=2时,ymin=0.∴x∈[1,2]时,函数的值域是![]() .
.
(3)∵F(x)=f(x)-f(-x)=![]() -
-![]() =2x.
=2x.
∴F(x)是奇函数.
证明:∵F(-x)=2(-x)=-2x=-F(x),
∴F(x)=2x是奇函数.
点睛:本题考查求函数的解析式,函数的值域以及函数的奇偶性. 二次函数在闭区间上必有最大值和最小值,它只能在区间的端点或二次函数图象的顶点处取到;常见题型有:(1)轴固定区间也固定;(2)轴动(轴含参数),区间固定;(3)轴固定,区间动(区间含参数). 找最值的关键是:(1)图象的开口方向;(2)对称轴与区间的位置关系;(3)结合图象及单调性确定函数最值.


科目:高中数学 来源: 题型:
【题目】已知圆![]() .
.
(1)若不经过坐标原点的直线![]() 与圆
与圆![]() 相切,且直线
相切,且直线![]() 在两坐标轴上的截距相等,求直线
在两坐标轴上的截距相等,求直线![]() 的方程;
的方程;
(2)设点![]() 在圆
在圆![]() 上,求点
上,求点![]() 到直线
到直线![]() 距离的最大值与最小值.
距离的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)若![]() 和
和![]() 在区间
在区间![]() 内具有相同的单调性,求实数
内具有相同的单调性,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,且函数
,且函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设铁路![]() 长为
长为![]() ,且
,且![]() ,为将货物从
,为将货物从![]() 运往
运往![]() ,现在
,现在![]() 上的距点
上的距点![]() 为
为![]() 的点
的点![]() 处修一公路至
处修一公路至![]() ,已知单位距离的铁路运费为
,已知单位距离的铁路运费为![]() ,公路运费为
,公路运费为![]() .
.
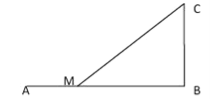
(1)将总运费![]() 表示为
表示为![]() 的函数;
的函数;
(2)如何选点![]() 才使总运费最小?
才使总运费最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数![]() 是奇函数
是奇函数
(1)求![]() 的值
的值
(2)判断f(x)在![]() 上的单调性。(直接写出答案,不用证明)
上的单调性。(直接写出答案,不用证明)
(3)若对于任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考四川文科】已知数列{![]() }的首项为1,
}的首项为1,![]() 为数列
为数列![]() 的前n项和,
的前n项和,![]() ,其中q>0,
,其中q>0,![]() .
.
(Ⅰ)若![]() 成等差数列,求
成等差数列,求![]() 的通项公式;
的通项公式;
(Ⅱ)设双曲线![]() 的离心率为
的离心率为![]() ,且
,且![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在颈椎病患者越来越多,甚至大学生也出现了颈椎病,年轻人患颈椎病多与工作、生活方式有关,某调查机构为了了解大学生患有颈椎病是否与长期过度使用电子产品有关,在遂宁市中心医院随机的对入院的50名大学生进行了问卷调查,得到了如下的4×4列联表:
未过度使用 | 过度使用 | 合计 | |
未患颈椎病 | 15 | 5 | 20 |
患颈椎病 | 10 | 20 | 30 |
合计 | 25 | 25 | 50 |
(1)是否有99.5%的把握认为大学生患颈锥病与长期过度使用电子产品有关?
(2)已知在患有颈锥病的10名未过度使用电子产品的大学生中,有3名大学生又患有肠胃炎,现在从上述的10名大学生中,抽取3名大学生进行其他方面的排查,记选出患肠胃炎的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据与公式:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com