
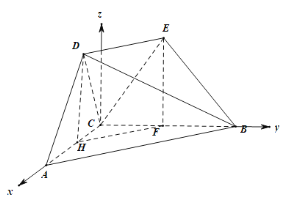
【题目】如图,在多面体ABCDE中,DE∥AB,AC⊥BC,BC=2AC=2,AB=2DE,且D点在平面ABC内的正投影为AC的中点H且DH=1.

(1)证明:面BCE⊥面ABC
(2)求BD与面CDE夹角的余弦值.
【答案】(1)证明见解析(2)![]() .
.
【解析】
(1)证明:取BC的中点F,连接EF,HF.证明四边形DEFH为平行四边形.然后证明DH⊥平面ABC,即可证明面ECB⊥面ABC.
(2)以C为原点,建立空间直角坐标系,求出平面CDE的法向量,求出![]() ,然后通过空间向量的数量积求解即可.
,然后通过空间向量的数量积求解即可.
(1)证明:取BC的中点F,连接EF,HF.
∵H,F分别为AC,BC的中点,
∴HF∥AB,且AB=2HF.
又DE∥AB,AB=2DE,
∴HF∥DE且HF=DE,
∴四边形DEFH为平行四边形.
∴EF∥DH,
又D点在平面ABC内的正投影为AC的中点H,
∴DH⊥平面ABC,
∴EF⊥平面ABC,
∵EF面BCE
∴面ECB⊥面ABC.

(2)解:∵DH⊥平面ABC,AC⊥BC,
∴以C为原点,建立空间直角坐标系,
则B(0,2,0),D(![]() ,0,1),E(0,1,1)
,0,1),E(0,1,1)
设平面CDE的法向![]() (x,y,z),
(x,y,z),![]() (
(![]() ,0,1),
,0,1),![]() (0,1,1),
(0,1,1),
则 ,取y=1,则x=2,z=﹣1.
,取y=1,则x=2,z=﹣1.
∴![]() ,
,
∵![]() ,设BD与面CDE夹角为
,设BD与面CDE夹角为![]() ,
,
∴ ,
,
∴BD与面CDE夹角的余弦值为
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】己知函数![]() 的定义域是
的定义域是![]() ,对任意的
,对任意的![]() ,有
,有![]() .当
.当![]() 时,
时,![]() .给出下列四个关于函数
.给出下列四个关于函数![]() 的命题:
的命题:
①函数![]() 是奇函数;
是奇函数;
②函数![]() 是周期函数;
是周期函数;
③函数![]() 的全部零点为
的全部零点为![]() ,
,![]() ;
;
④当算![]() 时,函数
时,函数![]() 的图象与函数
的图象与函数![]() 的图象有且只有4个公共点.
的图象有且只有4个公共点.
其中,真命题的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成的标准:年龄中位数在20岁以下为“年轻型”人口;年龄中位数在20~30岁为“成年型”人口;年龄中位数在30岁以上为“老龄型”人口.

如图反映了我国全面放开二孩政策对我国人口年龄中位数的影响.据此,对我国人口年龄构成的类型做出如下判断:①建国以来直至2000年为“成年型”人口;②从2010年至2020年为“老龄型”人口;③放开二孩政策之后我国仍为“老龄型”人口.其中正确的是( )
A.②③B.①③C.②D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,![]() ,E、F分别为AD,BC的中点.以EF为折痕把四边形EFCD折起,使点C到达点M的位置,点D到达点N的位置,且
,E、F分别为AD,BC的中点.以EF为折痕把四边形EFCD折起,使点C到达点M的位置,点D到达点N的位置,且![]() .
.

(1)求证:![]() 平面NEB;
平面NEB;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P-ABCD中,底面ABCD为菱形,且![]() ,侧面PAD是正三角形,其所在的平面垂直于底面ABCD,点G为AD的中点.
,侧面PAD是正三角形,其所在的平面垂直于底面ABCD,点G为AD的中点.

(1)求证:BG![]() 面PAD;
面PAD;
(2)E是BC的中点,在PC上求一点F,使得PG![]() 面DEF.
面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂包装白糖的生产线,正常情况下生产出来的白糖质量服从正态分布![]() (单位:
(单位:![]() ).
).
(Ⅰ)求正常情况下,任意抽取一包白糖,质量小于![]() 的概率约为多少?
的概率约为多少?
(Ⅱ)该生产线上的检测员某天随机抽取了两包白糖,称得其质量均小于![]() ,检测员根据抽检结果,判断出该生产线出现异常,要求立即停产检修,检测员的判断是否合理?请说明理巾.
,检测员根据抽检结果,判断出该生产线出现异常,要求立即停产检修,检测员的判断是否合理?请说明理巾.
附:![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() .
.
(1)求证:数列![]() 等差数列;
等差数列;
(2)当![]() 时,记
时,记![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列?若存在,求出所有满足条件的数对
成等比数列?若存在,求出所有满足条件的数对![]() ;若不存在,请说明理由;
;若不存在,请说明理由;
(3)若数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 是公比为
是公比为![]() 的等比数列,求最小正整数
的等比数列,求最小正整数![]() ,使得当
,使得当![]() 时,
时,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com