
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数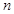 及天数如下表:
及天数如下表:
售出个数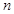 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
(1)0.5;(2)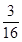 ;(3)分布列为
;(3)分布列为利润 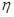
80 95 110 125 140 概率 
0.1 0.1 0.1 0.2 0.5
数学期望为123.5元.
解析试题分析:(1)由于小王某天售出该现烤面包超过13个的情况有三种:恰14个和恰15个,由题中表格易得:小王某天售出该现烤面包恰14个和恰15个的概率分别为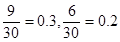 ,再由小王某天售出该现烤面包恰14个和恰15个这两个事件是互斥的,所以小王某天售出该现烤面包超过13个的概率就等于上述两个概率之和为:0.3+0.2=0.5.
,再由小王某天售出该现烤面包恰14个和恰15个这两个事件是互斥的,所以小王某天售出该现烤面包超过13个的概率就等于上述两个概率之和为:0.3+0.2=0.5.
(2)设在最近的5天中售出超过13个的天数为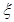 ,由于每天售出的个数要么超过13个,要么不超过13个只有这两种结果,且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变各为0.5,所以
,由于每天售出的个数要么超过13个,要么不超过13个只有这两种结果,且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变各为0.5,所以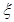 服从参数为5和0.5的二项分布,即
服从参数为5和0.5的二项分布,即 ,从而事件“小王增加订购量”的概率,即是
,从而事件“小王增加订购量”的概率,即是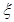 >3的概率,而
>3的概率,而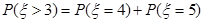 ,再由二项分布的概率公式
,再由二项分布的概率公式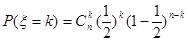 可算得事件“小王增加订购量”的概率;
可算得事件“小王增加订购量”的概率;
(3)由于小王每天订购14个现烤面包,则可设其一天的利润为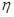 元,由已知求出
元,由已知求出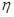 的所有可能取值,并结合题只所给条件可得到
的所有可能取值,并结合题只所给条件可得到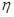 的每一个可能取值的概率,从而求得其分布列,在由数学期望公式:
的每一个可能取值的概率,从而求得其分布列,在由数学期望公式: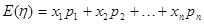 就可求得所获利润的数学期望.
就可求得所获利润的数学期望.
试题解析:(1)记事件A=“小王某天售出超过13个现烤面包”, 1分
用频率估计概率可知: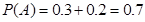 . 2分
. 2分
所以小王某天售出超过13个现烤面包的概率为0.5. 3分
(2)设在最近的5天中售出超过13个的天数为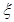 ,
,
则 . ..5分
. ..5分
记事件B=“小王增加订购量”,
则有 ,
,
所以小王增加订购量的概率为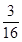 . 8分
. 8分
(3)若小王每天订购14个现烤面包,设其一天的利润为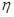 元,则
元,则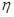 的所有可能取值为80,95,110,125,140. 9分
的所有可能取值为80,95,110,125,140. 9分
其分布列为
11分 利润 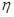
80 95 110 125 140 概率 
0.1 0.1 0.1 0.2 0.5
则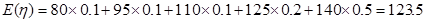
所以小王每天出售该现烤面包所获利润的数学期望为123.5元. ..13分
考点:1.概率和公式;2.二项分布;3.分布列与数学期望.


科目:高中数学 来源: 题型:解答题
甲有大小相同的两张卡片,标有数字2、3;乙有大小相同的卡片四张,分别标有1、2、3、4.
(1)求乙随机抽取的两张卡片的数字之和为奇数的概率;
(2)甲、乙分别取出一张卡,比较数字,数字大者获胜,求乙获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区为了解高二学生作业量和玩电脑游戏的情况,对该地区内所有高二学生采用随机抽样的方法,得到一个容量为200的样本.统计数据如下:
(1)已知该地区共有高二学生42500名,根据该样本估计总体,其中喜欢电脑游戏并认为作业不多的人有多少名?
(2)在A,B,C,D,E,F六名学生中,仅有A,B两名学生认为作业多.如果从这六名学生中随机抽取两名,求至少有一名学生认为作业多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,某中学甲、乙两班共有25名学生报名参加了一项 测试.这25位学生的考分编成的茎叶图,其中有一个数据因电脑操作员不小心删掉了(这里暂用x来表示),但他清楚地记得两班学生成绩的中位数相同.
(1)求这两个班学生成绩的中位数及x的值;
(2)如果将这些成绩分为“优秀”(得分在175分以上,包括175分)和“过关”,若学校再从这两个班获得“优秀”成绩的考生中选出3名代表学校参加比赛,求这3人中甲班至多有一人入选的概率.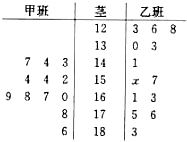
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
 .(12分)
.(12分) ,求
,求 的分布列与期望.
的分布列与期望. | 0.15 | 0.10 | 0.05[ | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 、
、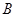 两盒中都有红球、白球,且球的形状、大小都相同,盒子
两盒中都有红球、白球,且球的形状、大小都相同,盒子 中有
中有 个红球与
个红球与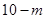 个白球,盒子
个白球,盒子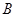 中有
中有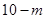 个红球与
个红球与 个白球(
个白球(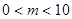 ).
).
(1)分别从 、
、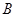 中各取一个球,
中各取一个球, 表示红球的个数;
表示红球的个数;
①请写出随机变量 的分布列,并证明
的分布列,并证明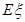 等于定值;
等于定值;
②当 为何值时,
为何值时,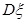 取到最小值,并求出最小值.
取到最小值,并求出最小值.
(2)在盒子 中不放回地摸取3个球,事件
中不放回地摸取3个球,事件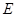 :在第一次取到红球后,以后两次都取到白球,事件
:在第一次取到红球后,以后两次都取到白球,事件 :在第一次取到白球后,以后两次都取到红球,若概率
:在第一次取到白球后,以后两次都取到红球,若概率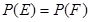 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛,假设每局甲获胜的概率为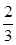 ,乙获胜的概率为
,乙获胜的概率为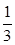 ,各局比赛结果相互独立.
,各局比赛结果相互独立.
求甲在4局以内(含4局)赢得比赛的概率;
记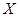 为比赛决出胜负时的总局数,求
为比赛决出胜负时的总局数,求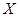 的分布列和均值(数学期望).
的分布列和均值(数学期望).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知向量a=(2,1),b=(x,y).
(1)若x∈{-1,0,1,2},y∈{-1,0,1},求向量a∥b的概率;
(2)若x∈[-1,2],y∈[-1,1],求向量a,b的夹角是钝角的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com