
【题目】已知圆C:(x﹣1)2+(y﹣2)2=4.
(1)求直线2x﹣y+4=0被圆C所截得的弦长;
(2)求过点M(3,1)的圆C的切线方程.
【答案】
(1)解:圆C:(x﹣1)2+(y﹣2)2=4的圆心为(1,2),半径长r=2,
圆心C(1,2)到直线2x﹣y+4=0的距离为: ![]() ,
,
所以直线2x﹣y+4=0被圆C所截得的弦长为: 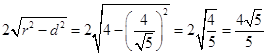
(2)解:因为(3﹣1)2+(1﹣2)2=5>4,所以点M在圆外,
当切线斜率存在时,设切线方称为:y﹣1=k(x﹣3)
即kx﹣y﹣3k+1=0,
圆心C(1,2)到直线kx﹣y﹣3k+1=0的距离为: ![]()
由题意有: ![]() ,所以
,所以 ![]()
此时切线方称为: ![]() ,即3x﹣4y﹣5=0,
,即3x﹣4y﹣5=0,
当切线斜率不存在时,直线x=3也与圆相切.
综上所述,所求切线方称为:3x﹣4y﹣5=0或x=3
【解析】(1)求出圆心C(1,2)到直线2x﹣y+4=0的距离,即可求直线2x﹣y+4=0被圆C所截得的弦长;(2)分类讨论,利用圆心C(1,2)到直线kx﹣y﹣3k+1=0的距离等于r,即可求过点M(3,1)的圆C的切线方程.


科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2+4ax+3a2<0,其中a≠0,命题q:实数x满足 ![]() .
.
(1)若a=﹣1,且p∨q为真,求实数x的取值范围;
(2)若¬p是¬q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论: ①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为(注:把你认为正确的结论的序号都填上).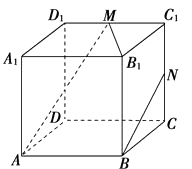
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中 ![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ![]() ,且图象上一个最低点为
,且图象上一个最低点为 ![]() . (Ⅰ)求f(x)的解析式;
. (Ⅰ)求f(x)的解析式;
(Ⅱ)当 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理健康教育老师对某班50个学生进行了心里健康测评,测评成绩满分为100分.成绩出来后,老师对每个成绩段的人数进行了统计,并得到如图4所示的频率分布直方图. 
(1)求a,并从频率分布直方图中求出成绩的众数和中位数;
(2)若老师从60分以下的人中选两个出来与之聊天,则这两人一个在(40,50]这一段,另一个在(50,60]这一段的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述: ①函数 ![]() 是奇函数;
是奇函数;
②函数 ![]() 的一条对称轴方程为
的一条对称轴方程为 ![]() ;
;
③函数 ![]() ,
, ![]() ,则f(x)的值域为
,则f(x)的值域为 ![]() ;
;
④函数 ![]() 有最小值,无最大值.
有最小值,无最大值.
所有正确结论的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com