
【题目】下列命题中错误的个数为:( )
①![]() 的图像关于点
的图像关于点![]() 对称;②
对称;②![]() 的图像关于点
的图像关于点![]() 对称;
对称;
③![]() 的图像关于直线
的图像关于直线![]() 对称;④
对称;④![]() 的图像关于直线
的图像关于直线![]() 对称。
对称。
A. 0 B. 1 C. 2 D. 3
【答案】B
【解析】
根据函数的奇偶性判断,①③,根据对称的定义:设对称中心的坐标为(a,b),则有2b=f(a+x)+f(a﹣x)对任意x均成立判断②,根据三角函数的图象 的性质判断④.
![]() ,f(﹣x)=
,f(﹣x)=![]() =
=![]() +
+![]() =
=![]() ﹣
﹣![]()
![]() =﹣f(x),
=﹣f(x),
∴函数为奇函数,则图象关于(0,0)对称,故正确;
y=x3-x-1的图象关于(0,-1)对称;
由题意设对称中心的坐标为(a,b),
则有2b=f(a+x)+f(a﹣x)对任意x均成立,代入函数解析式得,
2b=(a+x)3-(a+x)-1+(a﹣x)3-(a﹣x)-1对任意x均成立,
∴a=0,b=-1
即对称中心(0,-1),故不正确;
③y=![]() 的图象关于直线x=0对称,因为函数为偶函数,故函数关于y轴(x=0)对称,故正确,
的图象关于直线x=0对称,因为函数为偶函数,故函数关于y轴(x=0)对称,故正确,
④y=sinx+cosx=![]() sin(x+
sin(x+![]() )的图象关于直线x+
)的图象关于直线x+![]() =
=![]() 对称,即x=
对称,即x=![]() 对称,故正确.
对称,故正确.
故选:B.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 是自然对数的底数,
是自然对数的底数, ![]() =2.71828…).
=2.71828…).
(1)当![]() 时,过点
时,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() ,求
,求![]() 的方程;
的方程;
(2)当![]() 时,求证
时,求证![]() ;
;
(3)求证:对任意正整数![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
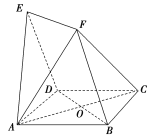
【题目】如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.
(1)求证:FC∥平面EAD;
(2)求二面角A-FC-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]()
(1)若![]() ,过点
,过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若曲线![]() 表示圆时,已知圆
表示圆时,已知圆![]() 与圆
与圆![]() 交于
交于![]() 两点,若弦
两点,若弦![]() 所在的直线方程为
所在的直线方程为![]() ,
, ![]() 为圆
为圆![]() 的直径,且圆
的直径,且圆![]() 过原点,求实数
过原点,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax3+bx2+cx+d的图象如图,则函数y=ax2+ ![]() bx+
bx+ ![]() 的单调递增区间是( )
的单调递增区间是( ) 
A.(﹣∞,2]
B.![]() ,+∞)
,+∞)
C.[﹣2,3]
D.![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. “sinθ=![]() ”是“θ=30°”的充分不必要条件
”是“θ=30°”的充分不必要条件
B. 命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0”
C. △ABC中,“sin A>sin B”是“A>B”的充要条件
D. 如果命题“綈p”与命题“p∨q”都是真命题,那么命题q一定是真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com