
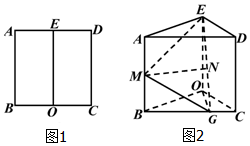
 如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.
如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.分析 (Ⅰ)取OG的中点的H,连结HN,HB,证明$HN=\frac{1}{2}OE$,推出四边形MNHB为平行四边形,得到MN∥BH,证明OE⊥平面OBC,然后推出OE⊥MN.
(Ⅱ)说明点M到平面OEG的距离为点B到平面OEG的距离,在三角形OBC中,推出∠OBG=30°,在△OBC中,求出BG=2,求出OG,然后求解点B到平面OEG的距离.
解答 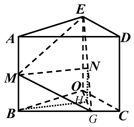 (本小题满分12分)
(本小题满分12分)
证明:(Ⅰ)如图6,取OG的中点的H,连结HN,HB,…(1分)
由N为EG中点,得△GOE中位线HN∥OE,且$HN=\frac{1}{2}OE$,
又BM∥OE,M为且AB中点,故$BM=\frac{1}{2}AB=\frac{1}{2}OE$,
∴HN∥BM,且HN=BM∴四边形MNHB为平行四边形,
∴MN∥BH.…(2分)
在正方形ABCD中,E、O分别为 AD、BC的中点
∴$\left\{\begin{array}{l}OE⊥OB\\ OE⊥OC\\ OB∩OC=O\end{array}\right.$得OE⊥平面OBC,…(3分)
又BH?平面OBC,∴OE⊥BH,∴OE⊥MN.…(5分)
(Ⅱ)解:∵在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点
∴AB∥OE,又OE?平面OEG,AB?平面OEG,∴AB∥平面OEG,…(6分)
∴点M到平面OEG的距离为点B到平面OEG的距离.…(7分)
在三角形OBC中,OB=OC=$\sqrt{3}$,∠BOC=120°,∴∠OBG=30°,
在△OBC中,由余弦定理得BC=3,又BG=2GC,∴BG=2,
同法由余弦定理得OG=1,…(9分)
∴OB2+OG2=BG2,即OB⊥OG.
由(Ⅰ)知OE⊥平面OBC,又OB?平面OBC,∴OE⊥OB,
又OE∩OG=O,∴BO⊥平面OEG,…(11分)
∴点B到平面OEG的距离为BO=$\sqrt{3}$.
即点M到平面OEG的距离为$\sqrt{3}$.…(12分)
点评 本题列出直线与平面垂直的性质定理的应用,点到平面的距离的求法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,+∞) | C. | $(1,\;\sqrt{2})$ | D. | $(\sqrt{2},\;+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 40 | C. | 30 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com