
ЎѕМвДїЎїФЪК®ѕЕґуЎ°ЅЁЙиГААцЦР№ъЎ±µДєЕХЩПВЈ¬ДіКЎј¶ЙъМ¬Е©ТµКѕ·¶ПШґуБ¦КµК©ВМЙ«ЙъІъ·Ѕ°ёЈ¬¶ФДіЦЦЕ©ІъЖ·µДЙъІъ·ЅКЅ·Ц±рЅшРРБЛјЧЎўТТБЅЦЦ·Ѕ°ёµДёДБјЎЈОЄБЛјмІйјЧЎўТТБЅЦЦ·Ѕ°ёµДёДБјР§№ыЈ¬Лж»ъФЪХвБЅЦЦ·Ѕ°ёЦРёчИОТвійИЎБЛ![]() јюІъЖ·ЧчОЄСщ±ѕЦрјюіЖіцЛьГЗµДЦШБїЈЁµҐО»ЈєїЛЈ©Ј¬ЦШБїЦµВдФЪ
јюІъЖ·ЧчОЄСщ±ѕЦрјюіЖіцЛьГЗµДЦШБїЈЁµҐО»ЈєїЛЈ©Ј¬ЦШБїЦµВдФЪ![]() Ц®јдµДІъЖ·ОЄєПёсЖ·Ј¬·сФтОЄІ»єПёсЖ·ЎЈПВ±нКЗјЧЎўТТБЅЦЦ·Ѕ°ёСщ±ѕЖµКэ·ЦІј±нЎЈ
Ц®јдµДІъЖ·ОЄєПёсЖ·Ј¬·сФтОЄІ»єПёсЖ·ЎЈПВ±нКЗјЧЎўТТБЅЦЦ·Ѕ°ёСщ±ѕЖµКэ·ЦІј±нЎЈ
ІъЖ·ЦШБї | јЧ·Ѕ°ёЖµКэ | ТТ·Ѕ°ёЖµКэ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЈЁ1Ј©ЗуіцјЧ(Н¬ЧйЦРµДЦШБїЦµУГЧйЦРµгЦµґъМж)·Ѕ°ёСщ±ѕЦР![]() јюІъЖ·µДЖЅѕщКэЈ»
јюІъЖ·µДЖЅѕщКэЈ»
ЈЁ2Ј©ИфТФЖµВКЧчОЄёЕВКЈ¬КФ№АјЖґУБЅЦЦ·Ѕ°ё·Ц±рИОИЎ![]() јюІъЖ·Ј¬ЗЎєГБЅјюІъЖ·¶јКЗєПёсЖ·µДёЕВК·Ц±рКЗ¶аЙЩЈ»
јюІъЖ·Ј¬ЗЎєГБЅјюІъЖ·¶јКЗєПёсЖ·µДёЕВК·Ц±рКЗ¶аЙЩЈ»
ЈЁ3Ј©УЙТФЙПНіјЖКэѕЭНкіЙПВГж![]() БРБЄ±нЈ¬Іў»ШґрУР¶аґу°СОХИПОЄЎ°ІъЖ·КЗ·сОЄєПёсЖ·УлёДБј·Ѕ°ёµДСЎФсУР№ШЎ±.
БРБЄ±нЈ¬Іў»ШґрУР¶аґу°СОХИПОЄЎ°ІъЖ·КЗ·сОЄєПёсЖ·УлёДБј·Ѕ°ёµДСЎФсУР№ШЎ±.
јЧ·Ѕ°ё | ТТ·Ѕ°ё | єПјЖ | |
єПёсЖ· | |||
І»єПёсЖ· | |||
єПјЖ |
ІОїј№«КЅЈє 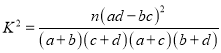 Ј¬ЖдЦР
Ј¬ЖдЦР![]() .
.
БЩЅзЦµ±нЈє
|
|
|
|
|
|
|
|
|
|
|
|
Ўѕґр°ёЎї(1) ![]() .
.
(2) ![]() .
.
(3)БРБЄ±нјыЅвОц; УР![]() µД°СОХИПОЄЎ°ІъЖ·ЦКБїУлёДБј·Ѕ°ёµДСЎФсУР№ШЎ±.
µД°СОХИПОЄЎ°ІъЖ·ЦКБїУлёДБј·Ѕ°ёµДСЎФсУР№ШЎ±.
ЎѕЅвОцЎї·ЦОцЈєЈЁ1Ј©УЙЖµВК·ЦІј±нЗуіцјЧ·Ѕ°ёСщ±ѕЦР40јюІъЖ·µДЖЅѕщКэєНЦРО»КэЈ»
ЈЁ2Ј©БРіц![]() БРБЄ±нЈ¬јЖЛг
БРБЄ±нЈ¬јЖЛг![]() Ј¬ёщѕЭБЩЅзЦµ±нёсЈ¬ЧчіцЕР¶П.
Ј¬ёщѕЭБЩЅзЦµ±нёсЈ¬ЧчіцЕР¶П.
ПкЅвЈє
ЈЁ1Ј©![]()
јЧµДЦРО»КэОЄ![]()
ЈЁ2Ј©ЙиґУјЧ·Ѕ°ёИОИЎ1јюІъЖ·ОЄєПёсЖ·ОЄКВјюAЈ¬Фт![]()
ЙиґУТТ·Ѕ°ёИОИЎ1јюІъЖ·ОЄєПёсЖ·ОЄКВјюBЈ¬Фт![]()
ЛщТФБЅјюІъЖ·ЗЎєГ¶јКЗєПёсЖ·µДёЕВКОЄ![]()
ЈЁ3Ј©![]() БРБЄ±н
БРБЄ±н
јЧ·Ѕ°ё | ТТ·Ѕ°ё | єПјЖ | |
єПёсЖ· | 30 | 36 | 66 |
І»єПёсЖ· | 10 | 4 | 14 |
єПјЖ | 40 | 40 | 80 |
ТтОЄ![]()
№КУР90%µД°СОХИПОЄЎ°ІъЖ·ЦКБїУлёДБј·Ѕ°ёµДСЎФсУР№ШЎ±.


 ЦРїјЅв¶Бїјµгѕ«Б·ПµБРґр°ё
ЦРїјЅв¶Бїјµгѕ«Б·ПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЖЅРРЛД±ЯРОABCDµДИэёц¶ҐµгµДЧш±кОЄ![]()
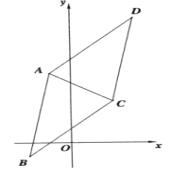
ЈЁ1Ј©ЗуЖЅРРЛД±ЯРОABCDµД¶ҐµгDµДЧш±кЈ»
ЈЁ2Ј©ЗуЛД±ЯРОABCDµДГж»э
ЈЁ3Ј©Зу![]() µДЖЅ·ЦПЯЛщФЪЦ±ПЯ·ЅіМЎЈ
µДЖЅ·ЦПЯЛщФЪЦ±ПЯ·ЅіМЎЈ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪУэГсЦРС§ѕЩРРµДµзДФЦЄК¶ѕєИьЦРЈ¬Ѕ«ѕЕДкј¶БЅёц°аІОИьµДС§ЙъіЙјЁ(µГ·ЦѕщОЄХыКэ)ЅшРРХыАнєу·ЦіЙОеЧйЈ¬»жЦЖИзНјЛщКѕµДЖµВК·ЦІјЦ±·ЅНјЈ®ТСЦЄНјЦРґУЧуµЅУТµДµЪТ»ЎўµЪИэЎўµЪЛДЎўµЪОеРЎЧйµДЖµВК·Ц±рКЗ0.30,0.15,0.10,0.05Ј¬µЪ¶юРЎЧйµДЖµКэКЗ40.
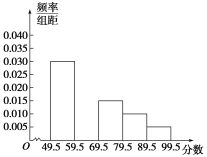
(1)ЗуµЪ¶юРЎЧйµДЖµВКЈ¬ІўІ№И«ХвёцЖµВК·ЦІјЦ±·ЅНјЈ»
(2)ЗуХвБЅёц°аІОИьµДС§ЙъИЛКэКЗ¶аЙЩЈї
(3)ЗуХвБЅёц°аІОИьС§ЙъµДіЙјЁµДЦРО»Кэ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() Ј¬
Ј¬![]() ФЪТ»ёцЦЬЖЪДЪµДНјПсИзНјЛщКѕ.
ФЪТ»ёцЦЬЖЪДЪµДНјПсИзНјЛщКѕ.
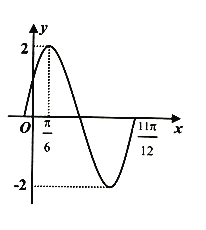
ЈЁIЈ©ЗуєЇКэ![]() µДЅвОцКЅЈ»
µДЅвОцКЅЈ»
ЈЁIIЈ©Йи![]() Ј¬ЗТ·ЅіМ
Ј¬ЗТ·ЅіМ![]() УРБЅёцІ»Н¬µДКµКэёщЈ¬ЗуКµКэ
УРБЅёцІ»Н¬µДКµКэёщЈ¬ЗуКµКэ![]() µДИЎЦµ·¶О§ТФј°ХвБЅёцёщµДєН.
µДИЎЦµ·¶О§ТФј°ХвБЅёцёщµДєН.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ
fЈЁxЈ©=ЈЁcosx©ЃxЈ©ЈЁ¦Р+2xЈ©©Ѓ ![]() ЈЁsinx+1Ј©
ЈЁsinx+1Ј©
gЈЁxЈ©=3ЈЁx©Ѓ¦РЈ©cosx©Ѓ4ЈЁ1+sinxЈ©lnЈЁ3©Ѓ ![]() Ј©
Ј©
Ц¤ГчЈє
ЈЁ1Ј©ґжФЪОЁТ»x0ЎКЈЁ0Ј¬ ![]() Ј©Ј¬К№fЈЁx0Ј©=0Ј»
Ј©Ј¬К№fЈЁx0Ј©=0Ј»
ЈЁ2Ј©ґжФЪОЁТ»x1ЎКЈЁ ![]() Ј¬¦РЈ©Ј¬К№gЈЁx1Ј©=0Ј¬ЗТ¶ФЈЁўсЈ©ЦРµДx0 Ј¬ УРx0+x1Јј¦РЈ®
Ј¬¦РЈ©Ј¬К№gЈЁx1Ј©=0Ј¬ЗТ¶ФЈЁўсЈ©ЦРµДx0 Ј¬ УРx0+x1Јј¦РЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ ![]() Ј®
Ј®
ЈЁ1Ј©УГОеµгЧчНј·Ё»іц![]() ФЪі¤¶ИОЄТ»ёцЦЬЖЪµДЗшјдЙПµДНјПуЈ»
ФЪі¤¶ИОЄТ»ёцЦЬЖЪµДЗшјдЙПµДНјПуЈ»

ЈЁ2Ј©Ј©ЗуєЇКэ![]() µДµҐµчµЭФцЗшјдЈ»
µДµҐµчµЭФцЗшјдЈ»
ЈЁ3Ј©јтКцИзєОУЙ![]() µДНјПуѕ№эККµ±µДНјПу±д»»µГµЅ
µДНјПуѕ№эККµ±µДНјПу±д»»µГµЅ![]() µДНјПуЈї
µДНјПуЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() Ј®
Ј®
ЈЁ1Ј©µ±![]() К±Ј¬єЇКэ
К±Ј¬єЇКэ![]() ЗЎУРБЅёцІ»Н¬µДБгµгЈ¬ЗуКµКэ
ЗЎУРБЅёцІ»Н¬µДБгµгЈ¬ЗуКµКэ![]() µДЦµЈ»
µДЦµЈ»
ЈЁ2Ј©µ±![]() К±Ј¬
К±Ј¬
ўЩ Иф¶ФУЪИОТв![]() Ј¬єгУР
Ј¬єгУР![]() Ј¬Зу
Ј¬Зу![]() µДИЎЦµ·¶О§Ј»
µДИЎЦµ·¶О§Ј»
ўЪ Иф![]() Ј¬ЗуєЇКэ
Ј¬ЗуєЇКэ![]() ФЪЗшјд
ФЪЗшјд![]() ЙПµДЧоґуЦµ
ЙПµДЧоґуЦµ![]() Ј®
Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄ¦БЎКЈЁ ![]() Ј¬¦РЈ©Ј¬sin¦Б=
Ј¬¦РЈ©Ј¬sin¦Б= ![]() Ј®
Ј®
ЈЁ1Ј©ЗуsinЈЁ ![]() +¦БЈ©µДЦµЈ»
+¦БЈ©µДЦµЈ»
ЈЁ2Ј©ЗуcosЈЁ ![]() ©Ѓ2¦БЈ©µДЦµЈ®
©Ѓ2¦БЈ©µДЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЅ»НЁЦёКэКЗЦёЅ»НЁУµ¶ВЦёКэµДјтіЖЈ¬КЗЧЫєП·ґУіµАВ·Нші©НЁ»тУµ¶ВµДёЕДоРФЦёКэЦµЈ¬јЗЅ»НЁЦёКэОЄ![]() Ј¬Жд·¶О§ОЄ
Ј¬Жд·¶О§ОЄ![]() Ј¬·Ц±рУРОеёцј¶±рЈє
Ј¬·Ц±рУРОеёцј¶±рЈє![]() Ј¬і©НЁЈ»
Ј¬і©НЁЈ»![]() Ј¬»щ±ѕі©НЁЈ»
Ј¬»щ±ѕі©НЁЈ»![]() Ј¬Зб¶ИУµ¶ВЈ»
Ј¬Зб¶ИУµ¶ВЈ»![]() Ј¬ЦР¶ИУµ¶ВЈ»
Ј¬ЦР¶ИУµ¶ВЈ»![]() Ј¬СПЦШУµ¶В.ФЪНнёЯ·еК±¶ОЈЁ
Ј¬СПЦШУµ¶В.ФЪНнёЯ·еК±¶ОЈЁ![]() Ј©Ј¬ґУДіКРЅ»НЁЦё»УЦРРДСЎИЎБЛКРЗш20ёцЅ»НЁВ·¶ОЈ¬ТАѕЭЖдЅ»НЁЦёКэКэѕЭ»жЦЖµДЖµВК·ЦІјЦ±·ЅНјИзНјЛщКѕ.
Ј©Ј¬ґУДіКРЅ»НЁЦё»УЦРРДСЎИЎБЛКРЗш20ёцЅ»НЁВ·¶ОЈ¬ТАѕЭЖдЅ»НЁЦёКэКэѕЭ»жЦЖµДЖµВК·ЦІјЦ±·ЅНјИзНјЛщКѕ.
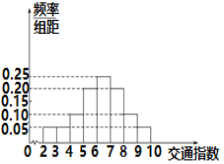
(1)ЗуіцЗб¶ИУµ¶ВЎўЦР¶ИУµ¶ВЎўСПЦШУµ¶ВµДВ·¶ОµДёцКэЈ»
(2)УГ·ЦІгійСщµД·Ѕ·ЁґУЗб¶ИУµ¶ВЎўЦР¶ИУµ¶ВЎўСПЦШУµ¶ВµДВ·¶ОЦР№ІійИЎ6ёцВ·¶ОЈ¬ЗуТАґОійИЎµДИэёцј¶±рВ·¶ОµДёцКэЈ»
(3)ґУ(2)ЦРійИЎµД6ёцВ·¶ОЦРИОИЎ2ёцЈ¬ЗуЦБЙЩУР1ёцВ·¶ООЄЗб¶ИУµ¶ВµДёЕВК.
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com