
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,试讨论函数
,试讨论函数![]() 的单调性;
的单调性;
(Ⅱ)设![]() ,当
,当![]() 对任意的
对任意的![]() 恒成立时,求函数
恒成立时,求函数![]() 的最大值的取值范围.
的最大值的取值范围.
【答案】(I)详见解析;(II)![]() .
.
【解析】试题分析:(Ⅰ)求导得![]() .结合
.结合![]() ,可得
,可得![]() 在
在![]() 上递减,在
上递减,在![]() 上递增.
上递增.
(Ⅱ)由![]() 对任意的
对任意的![]() 恒成立 可得
恒成立 可得![]() .又由(Ⅰ)知,当
.又由(Ⅰ)知,当![]() 时,
时, 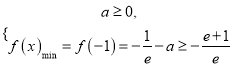 ,可得
,可得![]()
对![]() 求导,研究其最值,并求其范围即可
求导,研究其最值,并求其范围即可
试题解析:
(Ⅰ)![]() .
.
因为![]() ,则
,则![]() 时
时![]() 时
时![]() ,
,
∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增.
上递增.
(Ⅱ)当![]() 时,若
时,若![]() ,则
,则![]() .
.
所以![]() 对任意的
对任意的![]() 恒成立 ,
恒成立 , ![]() .
.
由(Ⅰ)知,当![]() 时,
时, ![]() 在
在![]() 上递减,在
上递减,在![]() 上递增.
上递增.
依题意,有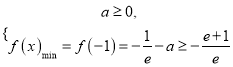 ,∴
,∴![]()
![]() .
.
∴![]() .
.
设![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上递增,
上递增,
∵![]() ,
, ![]() .
.
因此,存在唯一![]() ,使得
,使得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递减.
单调递减.
因此![]() 在
在![]() 处取得最大值,最大值为
处取得最大值,最大值为
![]() ,
, ![]()
设![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上递减,∴
上递减,∴![]() ,∴
,∴![]()
∴![]() 时
时![]() 的最大值
的最大值![]() .
.
反之,任取![]() ,下证
,下证![]() ,
, ![]()
∵![]() 在
在![]() 上递减,在
上递减,在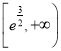 上递增,且
上递增,且![]() 时
时![]() ,
,
∴任取![]() ,存在唯一的
,存在唯一的![]() ,使得
,使得![]() .
.
∵![]() ,∴
,∴![]() 在
在![]() 上递减,
上递减,
∴![]() 时,
时, ![]() .
.
综上,当![]() 对任意的
对任意的![]() 恒成立时,函数
恒成立时,函数![]() 最大值,最大值的取值范围为
最大值,最大值的取值范围为![]() .
.
注:后半部分的证明是为了说明当![]() 在
在![]() 内变化时, 能取遍
内变化时, 能取遍![]() 内的所有值,从而
内的所有值,从而![]() 的最大值能取遍
的最大值能取遍![]() 内所有的值,防止把
内所有的值,防止把![]() 的最大值的取值范围变大.
的最大值的取值范围变大.


科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E、F分别为棱AB、AD的中点.
(1)求证:EF平行平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1
(3)求直线A1C与平面ABCD所成角的正切值.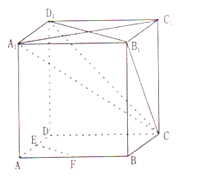
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨;生产乙种棉纱1吨需耗一级籽棉1吨,二级籽棉2吨.每1吨甲种棉纱的利润为900元,每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中,要求消耗一级籽棉不超过250吨,二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨,能使利润总额最大?并求出利润总额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】酒后违法驾驶机动车危害巨大,假设驾驶人员血液中的酒精含量为![]() (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当![]() 时,为酒后驾车;当
时,为酒后驾车;当![]() 时,为醉酒驾车.如图为某市交管部分在一次夜间行动中依法查出的
时,为醉酒驾车.如图为某市交管部分在一次夜间行动中依法查出的![]() 名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中
名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中![]() 人数包含
人数包含![]() ).
).
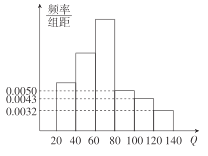
(Ⅰ)求查获的醉酒驾车的人数;
(Ⅱ)从违法驾车的![]() 人中按酒后驾车和醉酒驾车利用分层抽样抽取
人中按酒后驾车和醉酒驾车利用分层抽样抽取![]() 人做样本进行研究,再从抽取的
人做样本进行研究,再从抽取的![]() 人中任取
人中任取![]() 人,求
人,求![]() 人中含有醉酒驾车人数
人中含有醉酒驾车人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 (本小题满分12分)
如图, 在四面体ABOC中, ![]() , 且
, 且![]() .
.
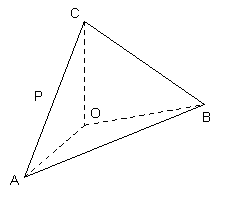
(Ⅰ)设为![]() 为
为![]() 的中点, 证明: 在
的中点, 证明: 在![]() 上存在一点
上存在一点![]() ,使
,使![]() ,并计算
,并计算![]() ;
;
(Ⅱ)求二面角![]() 的平面角的余弦值。
的平面角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值![]() ,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出
,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出![]() 的值为 ( )
的值为 ( )
(参考数据:![]() )
)
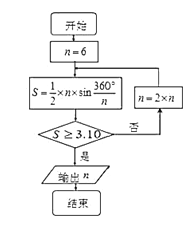
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学家刘徽在《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成的立体为“牟合方盖”,如图(1)(2),刘徽未能求得牟合方盖的体积,直言“欲陋形措意,惧失正理”,不得不说“敢不阙疑,以俟能言者”.约200年后,祖冲之的儿子祖暅提出“幂势既同,则积不容异”,后世称为祖暅原理,即:两等高立体,若在每一等高处的截面积都相等,则两立体体积相等.如图(3)(4),祖暅利用八分之一正方体去掉八分之一牟合方盖后的几何体与长宽高皆为八分之一正方体的边长的倒四棱锥“等幂等积”,计算出牟合方盖的体积,据此可知,牟合方盖的体积与其外切正方体的体积之比为( )
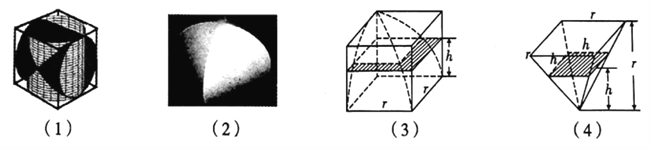
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com