
【题目】已知函数![]() .
.
(1) 解关于x的不等式![]() ;
;
(2) 若函数![]() 的图像恒在函数
的图像恒在函数![]() 图像的上方,求m的取值范围.
图像的上方,求m的取值范围.
【答案】(1)(-∞,a+1)∪(3-a,+∞);(2)(-∞,5).
【解析】
试题(1)本题是一个含参不等式的求解,需要按a=1,a>1,a<1进行讨论;(2)f(x)的图象恒在函数g(x)图象的上方,即为|x-2|>-|x+3|+m对任意实数x恒成立,分离参数为|x-2|+|x+3|>m恒成立.
所以对任意实数x恒有|x-2|+|x+3|≥|(x-2)-(x+3)|=5,于是得m<5.
试题解析:(1)不等式f(x)+a-1>0,
即|x-2|+a-1>0,
当a=1时,解集为x≠2,即(-∞,2)∪(2,+∞);
当a>1时,解集为全体实数R;
当a<1时,∵|x-2|>1-a,∴x-2>1-a或x-2<a-1,∴x>3-a或x<a+1,
故解集为(-∞,a+1)∪(3-a,+∞).
(2)f(x)的图象恒在函数g(x)图象的上方,即为|x-2|>-|x+3|+m对任意实数x恒成立,即|x-2|+|x+3|>m恒成立.
又对任意实数x恒有|x-2|+|x+3|≥|(x-2)-(x+3)|=5,于是得m<5,
即m的取值范围是(-∞,5).


科目:高中数学 来源: 题型:
【题目】天坛公园是明、清两代皇帝“祭天”“祈谷”的场所.天坛公园中的圜丘台共有三层(如图1所示),上层坛的中心是一块呈圆形的大理石板,从中心向外围以扇面形石(如图2所示).上层坛从第一环至第九环共有九环,中层坛从第十环至第十八环共有九环,下层坛从第十九环至第二十七环共有九环;第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块,则第二十七环的扇面形石块数是______;上、中、下三层坛所有的扇面形石块数是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】顺次连接椭圆![]() 的四个顶点恰好构成了一个边长为
的四个顶点恰好构成了一个边长为![]() 且面积为
且面积为![]() 的菱形。
的菱形。
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个不同点,若直线
上的两个不同点,若直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() (以
(以![]() 为坐标原点),线段
为坐标原点),线段![]() 上有一点
上有一点![]() 满足
满足![]() ,连接并延长交椭圆
,连接并延长交椭圆![]() 于点
于点![]() ,求椭圆
,求椭圆![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an} 满足a1=a,![]() =can+1﹣c(n∈N*),其中a、c为实数,且c≠0.
=can+1﹣c(n∈N*),其中a、c为实数,且c≠0.
(1)求数列{an} 的通项公式;
(2)设a=![]() ,c=
,c=![]() ,bn=n(1﹣an)(n∈N*),求数列 {bn}的前n项和Sn.
,bn=n(1﹣an)(n∈N*),求数列 {bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,点
,点![]() 是椭圆上的一个动点,
是椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)已知点![]() ,问是否存在直线
,问是否存在直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,若存在,求出直线
,若存在,求出直线![]() 斜率的取值范围;若不存在,说明理由.
斜率的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( ).
①“若![]() ,则
,则![]() ,
,![]() 中至少有一个不小于2”的逆命题是真命题;
中至少有一个不小于2”的逆命题是真命题;
②命题“设![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”是一个真命题;
”是一个真命题;
③命题![]() ,
,![]() ,则
,则![]() 是
是![]() 的必要不充分条件;
的必要不充分条件;
④命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”.
”.
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABC-A1B1C1中,底面ABC是边长为2的等边三角形,上、下底面的面积之比为1:4,侧面A1ABB1⊥底面ABC,并且A1A=A1B1,∠AA1B=90°.
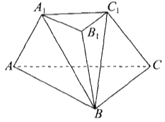
(1)平面A1C1B∩平面ABC=l,证明:A1C1∥l;
(2)求四棱锥B-A1ACC1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 在左、右焦点分别为
在左、右焦点分别为![]() ,
,![]() ,上顶点为点
,上顶点为点![]() ,若
,若![]() 是面积为
是面积为![]() 的等边三角形.
的等边三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,
,![]() 是椭圆
是椭圆![]() 上的两点,且
上的两点,且![]() ,求使
,求使![]() 的面积最大时直线
的面积最大时直线![]() 的方程(
的方程(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com