
【题目】已知方程(2+λ)x-(1+λ)y-2(3+2λ)=0与点P(-2,2).
(1)证明:对任意的实数λ,该方程都表示直线,且这些直线都经过同一定点,并求出这一定点的坐标;
(2)证明:该方程表示的直线与点P的距离d小于![]() .
.
【答案】(1)证明见解析;直线经过的定点为M(2,-2)(2)证明见解析
【解析】
(1)变形得到2x-y-6+λ(x-y-4)=0,得到方程![]() 计算得到答案.
计算得到答案.
(2)易知![]() ≤|PM|=
≤|PM|=![]() ,当
,当![]() 与直线垂直时,直线方程为x-y-4=0.,而直线系不能表示此直线,故得证.
与直线垂直时,直线方程为x-y-4=0.,而直线系不能表示此直线,故得证.
(1)解显然2+λ与-(1+λ)不可能同时为零,故对任意的实数λ,该方程都表示直线.
∵方程可变形为2x-y-6+λ(x-y-4)=0,∴![]() 解得
解得![]()
故直线经过的定点为M(2,-2).
(2)证明:易知![]() ≤|PM|=
≤|PM|=![]() ,当且仅当
,当且仅当![]() 与直线垂直时,等号成立
与直线垂直时,等号成立
此时对应的直线方程是y+2=x-2,即x-y-4=0.
但直线系方程唯独不能表示直线x-y-4=0,∴![]() <
<![]() ,故所证成立.
,故所证成立.


科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)经过点![]() (平面直角坐标系
(平面直角坐标系![]() 中点)作直线
中点)作直线![]() 交曲线
交曲线![]() 于
于![]() ,
, ![]() 两点,若
两点,若![]() 恰好为线段
恰好为线段![]() 的三等分点,求直线
的三等分点,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·衢州调研)已知四棱锥P-ABCD的底面ABCD是菱形,∠ADC=120°,AD的中点M是顶点P在底面ABCD的射影,N是PC的中点.

(1)求证:平面MPB⊥平面PBC;
(2)若MP=MC,求直线BN与平面PMC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与相应的生产能耗
吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |

(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过去大多数人采用储蓄的方式将钱储蓄起来,以保证自己生活的稳定![]() 考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式
考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式![]() 随着金融业的发展,普通人能够使用的投资理财工具也多了起来
随着金融业的发展,普通人能够使用的投资理财工具也多了起来![]() 为了研究某种理财工具的使用情况,现对
为了研究某种理财工具的使用情况,现对![]() 年龄段的人员进行了调查研究,将各年龄段人数分成5组:
年龄段的人员进行了调查研究,将各年龄段人数分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到频率分布直方图:
,并整理得到频率分布直方图:
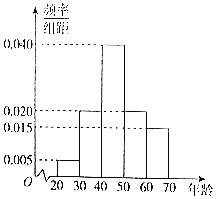
![]() Ⅰ
Ⅰ![]() 估计使用这种理财工具的人员年龄的中位数、平均数;
估计使用这种理财工具的人员年龄的中位数、平均数;
![]() Ⅱ
Ⅱ![]() 采用分层抽样的方法,从第二组、第三组、第四组中共抽取8人,则三个组中各抽取多少人?
采用分层抽样的方法,从第二组、第三组、第四组中共抽取8人,则三个组中各抽取多少人?
![]() Ⅲ
Ⅲ![]() 在
在![]() Ⅱ
Ⅱ![]() 中抽取的8人中,随机抽取2人,则第三组至少有1个人被抽到的概率是多少?
中抽取的8人中,随机抽取2人,则第三组至少有1个人被抽到的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 中,角A,B,C的对边为a,b,c,现给出以下四个命题:
中,角A,B,C的对边为a,b,c,现给出以下四个命题:
![]() 当
当![]() ,
,![]() ,
,![]() 时,满足条件的三角形共有1个;
时,满足条件的三角形共有1个;
![]() 若三角形a:b:
若三角形a:b:![]() :5:7,这个三角形的最大角是
:5:7,这个三角形的最大角是![]() ;
;
![]() 如果
如果![]() ,那么
,那么![]() 的形状是直角三角形;
的形状是直角三角形;
![]() 若
若![]() ,
,![]() ,
,![]() ,则
,则![]() 在
在![]() 方向的投影为
方向的投影为![]() .
.
以上命题中所有正确命题的序号是______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com